 steps (assuming exact arithmetic). Of
course this is of no practical value when
steps (assuming exact arithmetic). Of
course this is of no practical value when  is large; moreover, the
storage and computational requirements in the absence of restarts are
prohibitive. Indeed, the crucial element for successful application
of GMRES(
is large; moreover, the
storage and computational requirements in the absence of restarts are
prohibitive. Indeed, the crucial element for successful application
of GMRES(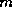 ) revolves around the decision of when to restart; that
is, the choice of
) revolves around the decision of when to restart; that
is, the choice of 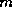 . Unfortunately, there exist examples for which
the method stagnates and convergence takes place only
at the
. Unfortunately, there exist examples for which
the method stagnates and convergence takes place only
at the  th step. For such systems, any choice of
th step. For such systems, any choice of 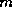 less than
less than  fails to converge.
fails to converge.
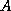 is real
and nearly positive definite, then a ``reasonable'' value for
is real
and nearly positive definite, then a ``reasonable'' value for