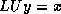 can be solved in the usual manner by introducing a
temporary vector
can be solved in the usual manner by introducing a
temporary vector  :
:
The system 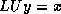 can be solved in the usual manner by introducing a
temporary vector
can be solved in the usual manner by introducing a
temporary vector  :
:

We have a choice between several equivalent ways of solving the system:
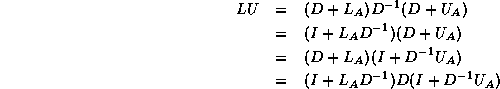
The first and fourth formulae are not suitable since they require
both multiplication and division with 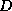 ; the difference between the
second and third is only one of ease of coding. In this section we use
the third formula; in the next section we will use the
second for the transpose system solution.
; the difference between the
second and third is only one of ease of coding. In this section we use
the third formula; in the next section we will use the
second for the transpose system solution.
Both halves of the solution have largely the same structure as the matrix vector multiplication.
for i = 1, n
sum = 0
for j = row_ptr(i), diag_ptr(i)-1
sum = sum + val(j) * z(col_ind(j))
end;
z(i) = pivots(i) * (x(i)-sum)
end;
for i = n, 1, (step -1)
sum = 0
for j = diag(i)+1, row_ptr(i+1)-1
sum = sum + val(j) * y(col_ind(j))
y(i) = z(i) - pivots(i) * sum
end;
end;
The temporary vector z can be eliminated by reusing the space
for y; algorithmically, z can even overwrite x, but overwriting input data is in general not recommended .