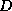 -
-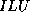 Incomplete Factorization
Incomplete Factorization
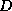 -
-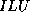 Incomplete Factorization
Incomplete Factorization
In this subsection we will consider
a matrix split as  in diagonal, lower and upper
triangular part, and an incomplete factorization preconditioner of the form
in diagonal, lower and upper
triangular part, and an incomplete factorization preconditioner of the form
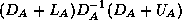 . In this way, we only need to store a
diagonal matrix
. In this way, we only need to store a
diagonal matrix 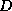 containing the pivots of the factorization.
containing the pivots of the factorization.
Hence,it suffices to allocate for the preconditioner only
a pivot array of length  (pivots(1:n)).
In fact, we will store the inverses of the pivots
rather than the pivots themselves. This implies that during
the system solution no divisions have to be performed.
(pivots(1:n)).
In fact, we will store the inverses of the pivots
rather than the pivots themselves. This implies that during
the system solution no divisions have to be performed.
Additionally, we assume that an extra integer array
diag_ptr(1:n)
has been allocated that contains the column (or row) indices of the
diagonal elements in each row, that is, 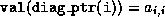 .
.
The factorization begins by copying the matrix diagonal
for i = 1, n
pivots(i) = val(diag_ptr(i))
end;
Each elimination step starts by inverting the pivot
for i = 1, n
pivots(i) = 1 / pivots(i)
For all nonzero elements  with
with  , we next check whether
, we next check whether
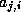 is a nonzero matrix element, since this is the only element
that can cause fill with
is a nonzero matrix element, since this is the only element
that can cause fill with  .
.
for j = diag_ptr(i)+1, row_ptr(i+1)-1
found = FALSE
for k = row_ptr(col_ind(j)), diag_ptr(col_ind(j))-1
if(col_ind(k) = i) then
found = TRUE
element = val(k)
endif
end;
If so, we update 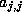 .
.
if (found = TRUE)
pivots(col_ind(j)) = pivots(col_ind(j))
- element * pivots(i) * val(j)
end;
end;