CRS-based Factorization Transpose Solve





Next: Generating a CRS-based
Up: Sparse Incomplete Factorizations
Previous: CRS-based Factorization Solve
Solving the transpose system 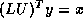 is slightly more involved. In the usual
formulation we traverse rows when solving a factored system, but here
we can only access columns of the matrices
is slightly more involved. In the usual
formulation we traverse rows when solving a factored system, but here
we can only access columns of the matrices 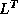 and
and 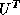 (at less
than prohibitive cost). The key idea is to distribute
each newly computed component of a triangular solve immediately over
the remaining right-hand-side.
(at less
than prohibitive cost). The key idea is to distribute
each newly computed component of a triangular solve immediately over
the remaining right-hand-side.
For instance, if we write a lower triangular matrix as
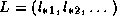 , then the system
, then the system 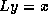 can be written as
can be written as
 . Hence, after computing
. Hence, after computing 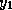 we modify
we modify
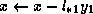 , and so on. Upper triangular systems are
treated in a similar manner.
With this algorithm we only access columns of the triangular systems.
Solving a transpose system with a matrix stored in CRS format
essentially means that we access rows of
, and so on. Upper triangular systems are
treated in a similar manner.
With this algorithm we only access columns of the triangular systems.
Solving a transpose system with a matrix stored in CRS format
essentially means that we access rows of 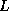 and
and 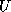 .
.
The algorithm now becomes
for i = 1, n
x_tmp(i) = x(i)
end;
for i = 1, n
z(i) = x_tmp(i)
tmp = pivots(i) * z(i)
for j = diag_ptr(i)+1, row_ptr(i+1)-1
x_tmp(col_ind(j)) = x_tmp(col_ind(j)) - tmp * val(j)
end;
end;
for i = n, 1 (step -1)
y(i) = pivots(i) * z(i)
for j = row_ptr(i), diag_ptr(i)-1
z(col_ind(j)) = z(col_ind(j)) - val(j) * y(i)
end;
end;
The extra temporary x_tmp is used only for clarity, and can
be overlapped with z. Both x_tmp and z can be
considered to be equivalent to y. Overall, a CRS-based
preconditioner solve uses short vector lengths, indirect addressing,
and has essentially the same memory traffic patterns as that of
the matrix-vector product.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
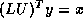 is slightly more involved. In the usual
formulation we traverse rows when solving a factored system, but here
we can only access columns of the matrices
is slightly more involved. In the usual
formulation we traverse rows when solving a factored system, but here
we can only access columns of the matrices 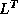 and
and 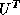 (at less
than prohibitive cost). The key idea is to distribute
each newly computed component of a triangular solve immediately over
the remaining right-hand-side.
(at less
than prohibitive cost). The key idea is to distribute
each newly computed component of a triangular solve immediately over
the remaining right-hand-side.
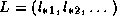 , then the system
, then the system 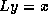 can be written as
can be written as
 . Hence, after computing
. Hence, after computing 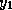 we modify
we modify
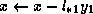 , and so on. Upper triangular systems are
treated in a similar manner.
With this algorithm we only access columns of the triangular systems.
Solving a transpose system with a matrix stored in CRS format
essentially means that we access rows of
, and so on. Upper triangular systems are
treated in a similar manner.
With this algorithm we only access columns of the triangular systems.
Solving a transpose system with a matrix stored in CRS format
essentially means that we access rows of 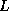 and
and 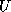 .
.