Choice of Grid Size




Next: Future Directions
Up: Performance
Previous: Choice of Block
The best grid shape is determined by the algorithm implemented in
the library and the underlying physical network. A one link physical
network will favor 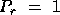 or
or 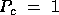 . This affects the scalabilty
of the algorithm, but reduces the overhead due to message collisions.
It is possible to predict the best grid shape given the number
of processes available. The current algorithms for the factorization
or reduction routines can be split into two categories.
. This affects the scalabilty
of the algorithm, but reduces the overhead due to message collisions.
It is possible to predict the best grid shape given the number
of processes available. The current algorithms for the factorization
or reduction routines can be split into two categories.
If at every step of the algorithm a block of columns and/or rows
needs to be broadcast, as in the LU or QR factorizations,
it is possible to pipeline this communication phase and overlap it
with some computation. The direction of the pipeline determines the
shape of the grid. For example, the LU, QR and QL factorizations
perform better for ``flat'' process grids ( ). These
factorizations share a common bottleneck of performing a reduction
operation along each column (for pivoting in LU, and for computing
a norm in QR and QL). The first implication of this observation
is that large latency message passing perform better on a ``flat''
grid than on a square grid. Secondly, after this reduction has been
performed, it is important to update the next block of columns as
fast as possible. This is done by broadcasting the current block of
columns using a ring topology, i.e, feeding the ongoing communication
pipe. Similarly, the performance of the LQ and RQ factorizations take
advantage of ``tall'' grids (
). These
factorizations share a common bottleneck of performing a reduction
operation along each column (for pivoting in LU, and for computing
a norm in QR and QL). The first implication of this observation
is that large latency message passing perform better on a ``flat''
grid than on a square grid. Secondly, after this reduction has been
performed, it is important to update the next block of columns as
fast as possible. This is done by broadcasting the current block of
columns using a ring topology, i.e, feeding the ongoing communication
pipe. Similarly, the performance of the LQ and RQ factorizations take
advantage of ``tall'' grids (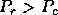 ) for the same reasons, but
transposed.
) for the same reasons, but
transposed.
The theoretical efficiency of the LU factorization can be estimated
by (see (1), (2)):

For large  , the last term in the denominator dominates, and it is
minimized by choosing a
, the last term in the denominator dominates, and it is
minimized by choosing a 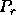 slightly smaller than
slightly smaller than 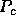 .
. 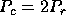 works
well on Intel machines. For smaller
works
well on Intel machines. For smaller  , the middle term dominates,
and it becomes more important to choose a small
, the middle term dominates,
and it becomes more important to choose a small 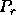 . Suppose that
we keep the ratio
. Suppose that
we keep the ratio 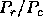 constant as
constant as 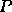 increases, thus we
have
increases, thus we
have 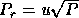 and
and  , where
, where  and
and  are constant [9]. Moreover, let ignore the
are constant [9]. Moreover, let ignore the  factor for a moment. In this case,
factor for a moment. In this case, 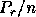 and
and  are proportional to
are proportional to  and
and 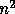 must grow with
must grow with 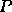 to maintain efficiency. For sufficient large
to maintain efficiency. For sufficient large 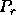 , the
, the  factor cannot be ignored, and the performance will slowly degrade
with the number of processors
factor cannot be ignored, and the performance will slowly degrade
with the number of processors 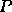 . This phenomenon is observed in
practice as shown in the plot above showing the efficiency of the
LU factorization on the Intel Paragon.
. This phenomenon is observed in
practice as shown in the plot above showing the efficiency of the
LU factorization on the Intel Paragon.

Click here to view the left figure
Click here to view the right figure
The second group of routines physically transpose a block of columns
and/or rows at every step of the algorithm. In these cases, it is not
usually possible to maintain a communication pipeline, and thus
square or near square grids are more optimal. This is the case for
the algorithms used for implementing the Cholesky factorization,
the matrix inversion and the reduction to bidiagonal form (BRD),
Hessenberg form (HRD) and tridiagonal form (TRD). For example,
the update phase of the Cholesky factorization of a lower symmetric
matrix physically transposes the current block of columns of the
lower triangular factor.
Assume now that at most 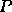 processes are available. A natural
question arising is: could we decide what process grid
processes are available. A natural
question arising is: could we decide what process grid
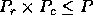 should be used? Similarly, depending
on
should be used? Similarly, depending
on 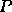 , it is not always possible to factor
, it is not always possible to factor 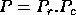 to
create the appropriate grid. For example, if
to
create the appropriate grid. For example, if 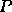 is prime, the
only possible grids are
is prime, the
only possible grids are  and
and  . If such
grids are particularly bad for performance, it may be beneficial
to let some processors remain idle, so the remainder can be formed
into a ``squarer'' grid [15].
These problems can be analyzed by a complicated function of the
machine and problem parameters. It is possible to develop models
depending on the machine and problem parameters which accurately
estimate the impact of modifying the shape of the grid on the total
execution time, as well as predicting the necessary amount of extra
memory required for each routine.
. If such
grids are particularly bad for performance, it may be beneficial
to let some processors remain idle, so the remainder can be formed
into a ``squarer'' grid [15].
These problems can be analyzed by a complicated function of the
machine and problem parameters. It is possible to develop models
depending on the machine and problem parameters which accurately
estimate the impact of modifying the shape of the grid on the total
execution time, as well as predicting the necessary amount of extra
memory required for each routine.




Next: Future Directions
Up: Performance
Previous: Choice of Block
Antoine Petitet
Fri Mar 31 13:01:26 EST 1995
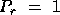 or
or 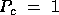 . This affects the scalabilty
of the algorithm, but reduces the overhead due to message collisions.
It is possible to predict the best grid shape given the number
of processes available. The current algorithms for the factorization
or reduction routines can be split into two categories.
. This affects the scalabilty
of the algorithm, but reduces the overhead due to message collisions.
It is possible to predict the best grid shape given the number
of processes available. The current algorithms for the factorization
or reduction routines can be split into two categories.
 ). These
factorizations share a common bottleneck of performing a reduction
operation along each column (for pivoting in LU, and for computing
a norm in QR and QL). The first implication of this observation
is that large latency message passing perform better on a ``flat''
grid than on a square grid. Secondly, after this reduction has been
performed, it is important to update the next block of columns as
fast as possible. This is done by broadcasting the current block of
columns using a ring topology, i.e, feeding the ongoing communication
pipe. Similarly, the performance of the LQ and RQ factorizations take
advantage of ``tall'' grids (
). These
factorizations share a common bottleneck of performing a reduction
operation along each column (for pivoting in LU, and for computing
a norm in QR and QL). The first implication of this observation
is that large latency message passing perform better on a ``flat''
grid than on a square grid. Secondly, after this reduction has been
performed, it is important to update the next block of columns as
fast as possible. This is done by broadcasting the current block of
columns using a ring topology, i.e, feeding the ongoing communication
pipe. Similarly, the performance of the LQ and RQ factorizations take
advantage of ``tall'' grids (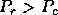 ) for the same reasons, but
transposed.
) for the same reasons, but
transposed.

 , the last term in the denominator dominates, and it is
minimized by choosing a
, the last term in the denominator dominates, and it is
minimized by choosing a 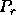 slightly smaller than
slightly smaller than 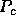 .
. 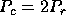 works
well on Intel machines. For smaller
works
well on Intel machines. For smaller 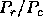 constant as
constant as 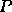 increases, thus we
have
increases, thus we
have 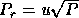 and
and  , where
, where  and
and  are constant
are constant  factor for a moment. In this case,
factor for a moment. In this case, 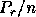 and
and  are proportional to
are proportional to  and
and 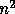 must grow with
must grow with 
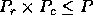 should be used? Similarly, depending
on
should be used? Similarly, depending
on 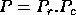 to
create the appropriate grid. For example, if
to
create the appropriate grid. For example, if  and
and  . If such
grids are particularly bad for performance, it may be beneficial
to let some processors remain idle, so the remainder can be formed
into a ``squarer'' grid
. If such
grids are particularly bad for performance, it may be beneficial
to let some processors remain idle, so the remainder can be formed
into a ``squarer'' grid