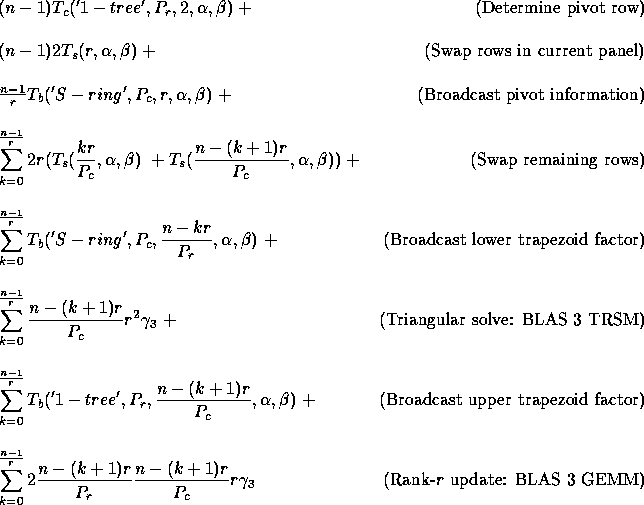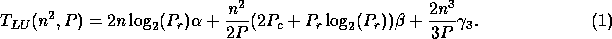The LU factorization on the DLAM




Next: Performance
Up: The Distributed Linear
Previous: Accuracy and Refinement
We present in this section the model corresponding to the parallel
right-looking LU factorization implemented in ScaLAPACK [9].
We restrict ourselves to the case where the matrix is distributed on
the processes using a square 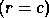 block cyclic decomposition scheme.
We ignore the possible collision of messages on the network. It can be
briefly described as follows: Assume the LU factorization of the
block cyclic decomposition scheme.
We ignore the possible collision of messages on the network. It can be
briefly described as follows: Assume the LU factorization of the
 first columns has proceeded with
first columns has proceeded with
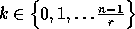 . During the next
step, the algorithm factors the next panel of
. During the next
step, the algorithm factors the next panel of  columns, pivoting if
necessary. Next the pivots are applied to the remainder of the matrix.
The lower trapezoid factor just computed is broadcast to the other
process columns of the grid using a split-ring topology
[10][8], so that the the upper trapezoid factor can be
updated via a triangular solve. This factor is then broadcast to the
other process rows using a 1-tree topology [10][8], so
that the remainder of the matrix can be updated by a rank-
columns, pivoting if
necessary. Next the pivots are applied to the remainder of the matrix.
The lower trapezoid factor just computed is broadcast to the other
process columns of the grid using a split-ring topology
[10][8], so that the the upper trapezoid factor can be
updated via a triangular solve. This factor is then broadcast to the
other process rows using a 1-tree topology [10][8], so
that the remainder of the matrix can be updated by a rank- update.
This process continues recursively with the updated matrix. The total
execution time
update.
This process continues recursively with the updated matrix. The total
execution time  can be estimated by
can be estimated by
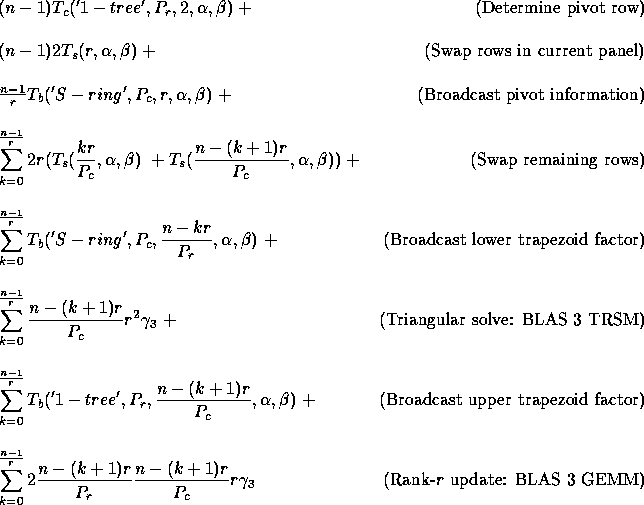
Notice that we neglected the BLAS 1 computations performed during the
factorization of the current panel of columns, considering that the
contribution of this operations to the execution time is mostly due
to communication. In addition, when the logical mesh can be embedded
into the physical network and the message collisions neglected, the
previous formula can be simplified to:
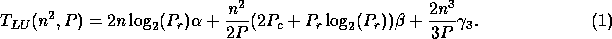
Antoine Petitet
Fri Mar 31 13:01:26 EST 1995
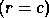 block cyclic decomposition scheme.
We ignore the possible collision of messages on the network. It can be
briefly described as follows: Assume the LU factorization of the
block cyclic decomposition scheme.
We ignore the possible collision of messages on the network. It can be
briefly described as follows: Assume the LU factorization of the
 first columns has proceeded with
first columns has proceeded with
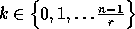 . During the next
step, the algorithm factors the next panel of
. During the next
step, the algorithm factors the next panel of  columns, pivoting if
necessary. Next the pivots are applied to the remainder of the matrix.
The lower trapezoid factor just computed is broadcast to the other
process columns of the grid using a split-ring topology
[10][8], so that the the upper trapezoid factor can be
updated via a triangular solve. This factor is then broadcast to the
other process rows using a 1-tree topology [10][8], so
that the remainder of the matrix can be updated by a rank-
columns, pivoting if
necessary. Next the pivots are applied to the remainder of the matrix.
The lower trapezoid factor just computed is broadcast to the other
process columns of the grid using a split-ring topology
[10][8], so that the the upper trapezoid factor can be
updated via a triangular solve. This factor is then broadcast to the
other process rows using a 1-tree topology [10][8], so
that the remainder of the matrix can be updated by a rank- update.
This process continues recursively with the updated matrix. The total
execution time
update.
This process continues recursively with the updated matrix. The total
execution time  can be estimated by
can be estimated by