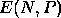 , for a problem of size
, for a problem of size 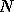 on
on
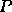 processors is defined in the usual way [13] as
processors is defined in the usual way [13] as
An important performance metric is
parallel efficiency.
Parallel efficiency, 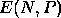 , for a problem of size
, for a problem of size 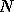 on
on
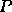 processors is defined in the usual way [13] as
processors is defined in the usual way [13] as
where 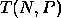 is the runtime of the parallel algorithm, and
is the runtime of the parallel algorithm, and
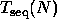 is the runtime of the best sequential algorithm.
An implementation is said to be scalable if the efficiency is
an increasing function of
is the runtime of the best sequential algorithm.
An implementation is said to be scalable if the efficiency is
an increasing function of 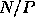 , the problem size per processor
(in the case of dense matrix computations,
, the problem size per processor
(in the case of dense matrix computations,  , the number
of words in the input).
, the number
of words in the input).
We will also measure the performance of our algorithm in
Megaflops/sec (or Gigaflops/sec). This is appropriate for large
dense linear algebra computations, since floating point dominates
communication. For a scalable algorithm with 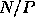 held fixed,
we expect the performance to be proportional to
held fixed,
we expect the performance to be proportional to 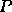 .
.
We seek to increase the performance of our algorithms by reducing overhead due to load imbalance, data movement, and algorithm restructuring. The way the data are distributed over the memory hierarchy of a computer is of fundamental importance to these factors. We present in this section extensive performance results on various platforms for the ScaLAPACK factorization and reductions routines. Performance data for the symmetric eigensolver (PDSYEVX) are presented in [5].