The Distributed Linear Algebra Machine (DLAM)




Next: The BLAS Process
Up:
ScaLAPACK: A Portable
Previous: Heterogeneous Networks
In this section, we present a theoretical model of a parallel computer
dedicated to dense linear algebra. This model is from an abstraction
of physical models. This ideal model provides a convenient
framework for developing parallel algorithms without worrying about
the implementation details or physical constraints. However, we defined
this restricted model such that actual code should be easily produced
from it.
The model can be applied to obtain theoretical performance bounds
on parallel computers or to estimate the execution time before or
after the algorithm has been implemented. The abstract model is
also useful in scalability and programmability analysis.
A 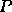 -process DLAM is constructed out of
-process DLAM is constructed out of 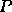 ``BLAS-processes''
interconnected by a logical ``BLACS-network''. This network is a
``BLAS-processes''
interconnected by a logical ``BLACS-network''. This network is a
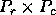 logical mesh such that
logical mesh such that 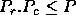 . Data
are exchanged between BLAS processes through the BLACS network by
calling BLACS primitives. The processes can only perform BLAS
and BLACS operations.
. Data
are exchanged between BLAS processes through the BLACS network by
calling BLACS primitives. The processes can only perform BLAS
and BLACS operations.
The DLAM presented here could be very easily extended by adding a
host process. This host process could act like a server acting
upon a user request, creating the BLACS-network, distributing the
data, starting the BLAS-processes and collecting the results. This
host process could also be used for fault-tolerant applications.
In this case, it would take the appropriate course of action in
the case of a BLAS-process failure. In the following sections,
however, we describe only the hostless DLAM.
Antoine Petitet
Fri Mar 31 13:01:26 EST 1995
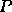 -process DLAM is constructed out of
-process DLAM is constructed out of 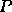 ``BLAS-processes''
interconnected by a logical ``BLACS-network''. This network is a
``BLAS-processes''
interconnected by a logical ``BLACS-network''. This network is a
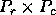 logical mesh such that
logical mesh such that 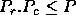 . Data
are exchanged between BLAS processes through the BLACS network by
calling BLACS primitives. The processes can only perform BLAS
and BLACS operations.
. Data
are exchanged between BLAS processes through the BLACS network by
calling BLACS primitives. The processes can only perform BLAS
and BLACS operations.