Rationale

In the design of all levels of the PBLAS, as with the BLAS, one of the main concerns is to keep both the calling sequences and the range of options limited, while at the same time maintaining sufficient functionality. This clearly implies a compromise, and a good judgement is vital if the PBLAS are to be accepted as a useful standard. In this section we discuss some of the reasoning behind the decisions we have made.

A large amount of sequential linear algebra software relies on the BLAS. Because software reusability is one of our major concerns, we wanted the BLAS and PBLAS interfaces to be as similar as possible. Consequently, only one routine, the matrix transposition, has been added to the PBLAS, since this operation is much more complex to perform in a distributed-memory environment [8].

One of the major differences between the BLAS and the PBLAS is likely to be found in the Level 1 routines. Indeed, the functions of the former have been replaced by subroutines in the latter. In our model implementation, the top-level routines are written in C, thus it was not possible to return a scalar anywhere else than in the argument list and at the same time to have the routines callable by C or FORTRAN programs. Moreover, it is useful for the PAMAX routines to return not only the value of the element of maximum absolute value but also its global index. This contradicts the principle that a function only returns a single value, thus the function became a subroutine.

The scalar values returned by the Level 1 PBLAS routines PDOT, PNRM2, PASUM and PAMAX are only correct in the scope of their operands and zero elsewhere. For example, when INCX is equal to one, only the column of processes having part of the vector operands gets the correct results. This decision was made for efficiency purposes. It is, however, very easy to have this information broadcast across the process mesh by directly calling the appropriate BLACS routine. Consequently, these particular routines do not need to be called by any other processes other than the ones in the scope of their operands. With this exception in mind, the PBLAS follow an SPMD programming model and need to be called by every process in the current BLACS context to work correctly.

Nevertheless, there are a few more exceptions in the current model implementation, where some computations local to a process row or column can be performed by the PBLAS, without having every process in the grid calling the routine. For example, the rank-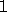 update performed in the LU factorization presented in the next section, involves data which is contained by only one process column. In this case, to maintain the efficiency of the factorization it is important to have this particular operation performed only within one process column. In other words, when a PBLAS routine is called by every process in the grid, it is required that the code operates successfully as specified by the SPMD programming model. However, it is also necessary that the PBLAS routines recognize the scope of their operands in order to save useless communication and synchronization costs when possible. This specific part of the PBLAS specifications remains an open question.

A few features supported by the PBLAS underlying tools [9] have been intentionally hidden. For instance, a block of identical vectors operands are sometimes replicated across process rows or columns. When such a situation occurs, it is possible to save some communication and computation operations. The PBLAS interface could provide such operations, for example, by setting the origin process coordinate in the array descriptor to -1 (see Sect. 3.2). Such features, for example, would be useful in the ScaLAPACK routines responsible for applying a block of Householder vectors to a matrix. Indeed, these Householder vectors need to be broadcast to every process row or column before being applied. Whether or not this feature should be supported by the PBLAS is still an open question.

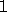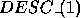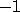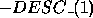We have adhered to the conventions of the BLAS in allowing an increment argument to be associated with each distributed vector so that a vector could, for example, be a row of a matrix. However, negative increments or any value other than or are not supported by our current model implementation. The negative increments and should be relatively easy to support. It is still unclear how it would be possible to take advantage of this added complexity and if other increment values should be supported.

The presence of BLACS contexts associated with every distributed matrix provides the ability to have separate ``universes'' of message passing. The use of separate communication contexts by distinct libraries (or distinct library invocations) such as the PBLAS insulates communication internal to the library execution from external communication. When more than one descriptor array is present in the argument list of a routine in the PBLAS, it is required that the BLACS context entries must be equal (see Sect. 3.3). In other words, the PBLAS do not perform ``intra-context'' operations.

We have not included specialized routines to take advantage of packed storage schemes for symmetric, Hermitian, or triangular matrices, nor of compact storage schemes for banded matrices. As with the BLAS no check has been included for singularity, or near singularity, in the routines for solving triangular systems of equations. The requirements for such a test depend on the application and so we felt that this should not be included, but should instead be performed outside the triangular solve.

For obvious software reusability reasons we have tried to adhere to the conventions of, and maintain consistency with, the sequential BLAS. However, we have deliberately departed from this approach by explicitly passing the global indices and using array descriptors. Indeed, it is our experience that using a ``local indexing'' scheme for the interface makes the use of these routines much more complex from the user's point of view. Our implementation of the PBLAS emphasizes the mathematical view of a matrix over its storage. In fact, other block distributions may be able to reuse both the interface and the descriptor described in this paper without change. Fundamentally different distributions may require modifications of the descriptor, but the interface should remain unchanged.

The model implementation in its current state provides sufficient functionality for the use of the PBLAS modules in the ScaLAPACK library. However, as we mentioned earlier in this paper, there are still a few details that remain open questions and may easily be accommodated as soon as more experience with these codes is reported. Hopefully, the comments and suggestions of the user community will help us to make these last decisions so that this proposal can be made more rigorous and adequate to the user's needs.

Finally, it is our experience that porting sequential code built on the top of the BLAS to distributed memory machines using the PBLAS is much simpler than writing the parallel code from scratch (see Sect. 7). Taking the BLAS proposals as our model for software design was in our opinion a way to ensure the same level of software quality for the PBLAS.