The order of the arguments of a PBLAS routine is as follows:
Note that every category is not present in each of the routines. The arguments that specify options are character arguments with the names SIDE, TRANS, TRANSA, TRANSB, UPLO and DIAG.
SIDE is used by the routines as follows:
TRANS, TRANSA and TRANSB are used by the routines as follows:
In the real case the values `T' and `C' have the same meaning, and in the complex case the value `T' is not allowed.
UPLO is used by the Hermitian, symmetric, and triangular distributed matrix routines to specify whether the upper or lower triangle is being referenced as follows:
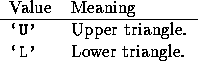
DIAG is used by the triangular distributed matrix routines to specify whether or not the distributed matrix is unit triangular, as follows:
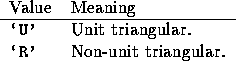
When DIAG is supplied as `U' the diagonal elements are not referenced.
Thus, these arguments have similar values and meanings as for the BLAS; TRANSA and TRANSB have the same values and meanings as TRANS, where TRANSA and TRANSB apply to the distributed matrix operands A and B respectively. We recommend that the equivalent lower case characters be accepted with the same meaning.
The distributed submatrix operands of the Level 3
PBLAS are determined by the arguments M,
N and K, which specify their size.
These numbers may differ from the two first
entries of the descriptor (M_ and
N_), which specifies the size of the
distributed matrix containing the submatrix operand.
Also required are the global starting indices IA,
JA, IB, JB, IC and JC.
It is permissible to call a routine with M or
N equal to zero, in which case the routine exits
immediately without referencing its distributed matrix
arguments. If M and N are greater than zero,
but K is equal to zero, the operation reduces to
C(IC:*,JC:*)
C(IC:*,JC:*)
(this applies to the GEMM, SYRK, SYR2K,
HERK and HER2K routines). The input-output
distributed submatrix (B(IB:*,JB:*) for the
TR-routines, C(IC:*,JC:*) otherwise) is
always M 
N if rectangular,
or N
N if square.
The description of the distributed matrix operands consists of
The description of a distributed vector operand is
similar to the description of a distributed matrix
(X, IX, JX, DESCX) followed by a global increment
INCX, which allows the selection of a matrix row
or a matrix column as a vector operand. Only two
increment values are currently supported by our model
implementation, namely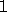 
to select a matrix column
and DESCX(1) (i.e INCX=MX) specifying a
matrix row.
The input scalars always have the dummy argument names ALPHA and BETA. Output scalars are only present in the Level 1 PBLAS and are called AMAX, ASUM, DOT, INDX and NORM2.
We use the description of two distributed matrix operands X and Y to describe the invalid values of the arguments:
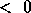or N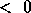 or K,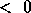
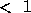or IX+M-1
M_ (= DESCX(1))
(assuming X(IX:IX+M-1,
) is to be operated on),
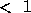or JX+N-1N_ (= DESCX(2)),
(assuming X(,JX:JX+N-1) is to be operated on),
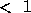or NB_ (=DESCX(4)),
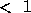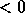or RSRC_
(number of process rows),
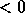or CSRC_
(number of process columns),
the local number of rows in the array
pointed to by X,
and INCX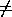
M_ (= DESCX(1))
(Only for vector operands),
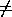CTXT_Y (=DESCY(7))
with X and Y distributed matrix operands.
If a routine is called with an invalid value for
any of its arguments, then it must report the fact
and terminate the execution of the program. In the
model implementation, each routine, on detecting an
error, calls a common error-handling routine
PBERROR(), passing to it the current BLACS
context, the name of the routine and the number of
the first argument that is in error. If an error is
detected in the j-th entry of a descriptor array,
which is the i-th argument in the parameter list, the
number passed to PBERROR() has been arbitrarily
chosen to be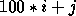 
. This allows the user to
distinguish an error on a descriptor entry from an
error on a scalar argument. For efficiency purposes,
the PBLAS routines only perform a local validity
check of their argument list. If an error is detected
in at least one process of the current context, the
program execution is stopped.
A global validity check of the input arguments passed to a PBLAS routine must be performed in the higher-level calling procedure. To demonstrate the need and cost of global checking, as well as the reason why this type of checking is not performed in the PBLAS, consider the following example: the value of a global input argument is legal but differs from one process to another. The results are unpredictable. In order to detect this kind of error situation, a synchronization point would be necessary, which may result in a significant performance degradation. Since every process must call the same routine to perform the desired operation successfully, it is natural and safe to restrict somewhat the amount of checking operations performed in the PBLAS routines.
Specialized implementations may call system-specific exception-handling facilities, either via an auxiliary routine PBERROR or directly from the routine. In addition, the testing programs can take advantage of this exception-handling mechanism by simulating specific erroneous input argument lists and then verifying that particular errors are correctly detected.