QR Factorization



Next: Cholesky Factorization
Up: Performance Results
Previous: LU Factorization
To obtain the elementary Householder vector 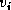 ,
the Euclidean norm of the vector,
,
the Euclidean norm of the vector, 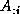 , is required.
The sequential LAPACK routine, DLARFG, calls the Level-1 BLAS
routine, DNRM2, which computes the norm while guarding against
underflow and overflow.
In the corresponding parallel ScaLAPACK routine, PDLARFG,
each process in the column of processes, which holds the vector,
, is required.
The sequential LAPACK routine, DLARFG, calls the Level-1 BLAS
routine, DNRM2, which computes the norm while guarding against
underflow and overflow.
In the corresponding parallel ScaLAPACK routine, PDLARFG,
each process in the column of processes, which holds the vector, 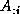 ,
computes the global norm safely using the PDNRM2 routine.
,
computes the global norm safely using the PDNRM2 routine.
For consistency with LAPACK, we have chosen to store  and
and 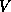 , and
generate
, and
generate  when necessary. Although storing
when necessary. Although storing  might save us some
redundant computation, we felt that consistency was more important.
might save us some
redundant computation, we felt that consistency was more important.
The 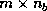 lower trapezoidal part of
lower trapezoidal part of 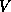 , which is a sequence of
the
, which is a sequence of
the 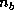 Householder vectors, will be accessed in the form,
Householder vectors, will be accessed in the form,

where 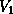 is
is 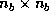 unit lower triangular, and
unit lower triangular, and
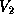 is
is 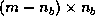 .
In the sequential routine, the multiplication involving
.
In the sequential routine, the multiplication involving 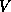 is divided
into two steps: DTRMM with
is divided
into two steps: DTRMM with 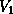 and DGEMM with
and DGEMM with 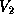 .
However, in the parallel implementation,
.
However, in the parallel implementation, 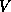 is contained in one column of
processes. Let
is contained in one column of
processes. Let 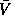 be a unit lower trapezoidal matrix containing
the strictly lower trapezoidal part of
be a unit lower trapezoidal matrix containing
the strictly lower trapezoidal part of 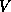 .
. 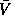 is broadcast
rowwise to the other process columns so that every column of processes
has its own copy. This allows us to perform the operations involving
is broadcast
rowwise to the other process columns so that every column of processes
has its own copy. This allows us to perform the operations involving
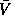 in one step (DGEMM), as illustrated in
Figure 7, and not worry about the upper
triangular part of
in one step (DGEMM), as illustrated in
Figure 7, and not worry about the upper
triangular part of 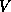 .
This one step multiplication not only simplifies the implementation of
the routine (PDLARFB), but may, depending upon the BLAS
implementation, increase the overall performance
of the routine (PDGEQRF) as well.
.
This one step multiplication not only simplifies the implementation of
the routine (PDLARFB), but may, depending upon the BLAS
implementation, increase the overall performance
of the routine (PDGEQRF) as well.
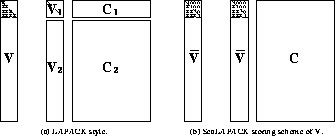
Figure 7: The storage scheme of the lower trapezoidal matrix 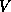 in ScaLAPACK QR factorization.
in ScaLAPACK QR factorization.

Figure 8: Performance of the QR factorization on the Intel iPSC/860,
Delta, and Paragon.
Figure 8 shows the performance of the QR factorization routine
on the Intel family of concurrent computers.
The block size of  was used on all of the machines.
Best performance was attained with an aspect ratio of
was used on all of the machines.
Best performance was attained with an aspect ratio of 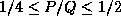 .
The highest performances of 3.1 Gflops for
.
The highest performances of 3.1 Gflops for 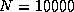 was obtained on the iPSC/860;
14.6 Gflops for
was obtained on the iPSC/860;
14.6 Gflops for 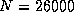 on the Delta; and 21.0 Gflops for
on the Delta; and 21.0 Gflops for 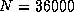 on the Paragon.
Generally, the QR factorization routine has the best performance
of the three factorizations
since the updating process of
on the Paragon.
Generally, the QR factorization routine has the best performance
of the three factorizations
since the updating process of 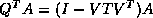 is rich in matrix-matrix operation, and the number of floating point
operations is the largest (
is rich in matrix-matrix operation, and the number of floating point
operations is the largest (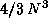 ).
).
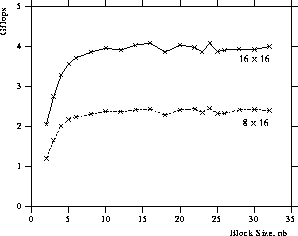
Figure 9: Performance of the Cholesky factorization
as a function of the block size on 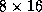 and
and 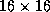 processes
of the Intel Delta (
processes
of the Intel Delta (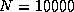 ).
).



Next: Cholesky Factorization
Up: Performance Results
Previous: LU Factorization
Susan Ostrouchov
Fri Apr 28 09:37:26 EDT 1995
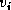 ,
the Euclidean norm of the vector,
,
the Euclidean norm of the vector, 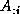 , is required.
The sequential LAPACK routine, DLARFG, calls the Level-1 BLAS
routine, DNRM2, which computes the norm while guarding against
underflow and overflow.
In the corresponding parallel ScaLAPACK routine, PDLARFG,
each process in the column of processes, which holds the vector,
, is required.
The sequential LAPACK routine, DLARFG, calls the Level-1 BLAS
routine, DNRM2, which computes the norm while guarding against
underflow and overflow.
In the corresponding parallel ScaLAPACK routine, PDLARFG,
each process in the column of processes, which holds the vector, 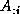 ,
computes the global norm safely using the PDNRM2 routine.
,
computes the global norm safely using the PDNRM2 routine.
 and
and 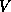 , and
generate
, and
generate  when necessary. Although storing
when necessary. Although storing 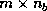 lower trapezoidal part of
lower trapezoidal part of 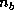 Householder vectors, will be accessed in the form,
Householder vectors, will be accessed in the form,
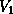 is
is 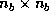 unit lower triangular, and
unit lower triangular, and
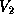 is
is 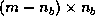 .
In the sequential routine, the multiplication involving
.
In the sequential routine, the multiplication involving 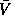 be a unit lower trapezoidal matrix containing
the strictly lower trapezoidal part of
be a unit lower trapezoidal matrix containing
the strictly lower trapezoidal part of 

 was used on all of the machines.
Best performance was attained with an aspect ratio of
was used on all of the machines.
Best performance was attained with an aspect ratio of 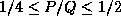 .
The highest performances of 3.1 Gflops for
.
The highest performances of 3.1 Gflops for 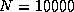 was obtained on the iPSC/860;
14.6 Gflops for
was obtained on the iPSC/860;
14.6 Gflops for 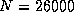 on the Delta; and 21.0 Gflops for
on the Delta; and 21.0 Gflops for 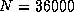 on the Paragon.
Generally, the QR factorization routine has the best performance
of the three factorizations
since the updating process of
on the Paragon.
Generally, the QR factorization routine has the best performance
of the three factorizations
since the updating process of 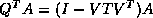 is rich in matrix-matrix operation, and the number of floating point
operations is the largest (
is rich in matrix-matrix operation, and the number of floating point
operations is the largest (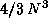 ).
).

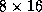 and
and 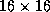 processes
of the Intel Delta (
processes
of the Intel Delta (