In this section, we develop formulae that give precise measures of the storage required for execution of a tile and of the number of data (input and output from local memory) required for execution of a tile. These can be used to state more precisely the optimization problem that should be solved in determining the tiling basis.
Consider I/O requirements first. Now, let E be an integer 
matrix whose columns represent the
data required to satisfy the true dependences in an index space.
Consider the loop nest
mmmmmmmmmm¯for i = 1 to n do
for j = 1 to n do
a[i,j] = a[i,j-1] + b[i,j-1] ; od
b[i,j] = a[i,j-1] + b[i-1,j-1] + c[i] ; od
od
In this loop nest, the dependences are
A given iteration requires one datum from the iteration at distance 
and two data from the iteration
at distance 
. Thus, the matrix E is
In addition to the data computed at other iterations in the index space,
for which dependence directions have been established, other data may be required in order to execute a tile,
for example, the c data in the example above. We express these data requirements through a second matrix,
C. Each column of C
corresponds to a datum (such as c[i] in the example) that is used in common by a number of iterations. It
gives the smallest displacement in the index space between iterations that use the datum.
For the example above,
since all iterations with fixed i use the value c[i]. If, for example, c0[i] were used for
and c1[i] were used at iterations 
, then we would have
We are now ready to state the I/O required to execute a tile.
We assume that no data are available in local memory to begin with and that all
data that may be needed later must be written back from local memory at completion of the tile's execution.
Let 
.
Let 
.
The amount of data is given by
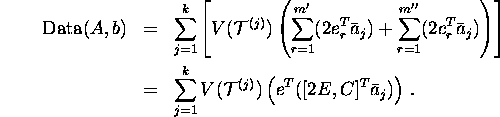
Here 
is the volume of the face of the tile normal to the tiling basis vector 
,
is a normalized tiling basis vector,
and 
.
That this is correct follows from the observation that the grid points at the face of a tile depend on values created
at iteration points in a ``shadow''; the shadow points are points not in the tile from which a dependence into the
tile emanates. For each column d of E the corresponding shadow has as its base a face of the tile, say the face
normal to , and as one of its sides the vector whose direction is -d and whose tail is at any corner
of the face. This shadow has height 
and base area , so it has volume 
.
The factor 2 multiplying E expresses the fact that data that are responsible for
dependences must be read in and written out, while data that are used but not created are read in but not written
back.
The volume of faces is explained in Section 2.3.