First, we note that if 
, then so is 
for any positive scalar 
.
The partition induced by A and b is unchanged if we scale the columns of A by arbitrary positive amount
and scale the corresponding components of b by the reciprocal amounts. There is therefore no loss of
generality if we replace A with 
, the matrix obtained by scaling the columns
of A to have unit euclidean length.
We first assume that 
.
Let 
.
Then except at the boundaries, all tiles are congruent to
is a parallelepiped subtended by the columns of the inverse of 
. In other words,
if 
, then
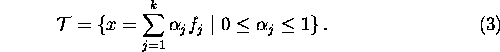
To see this, note that 
, so for any x that satisfies (3),
, and since 
, equation (2) is
satisfied.
Let 
denote the volume of . Then
Let us now consider the faces of . Without loss of generality, consider the face 
subtended by 
. The face is itself a (k-1) dimensional parallelepiped. We want to know
its surface area, or in general its (k-1) dimensional volume, which we denote 
.
We give a proof, unfortunately algebraic rather than geometric in nature, in the Appendix.
What are the consequences of the lemma? we see that all the faces have the same area and that it is
equal to the volume of . Thus, the ratio 
of the volume to the total surface area of is just the
reciprocal of the number of sides, 2k:
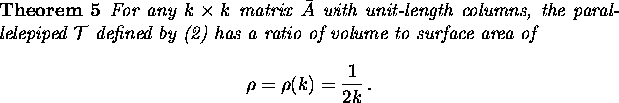
At first this is surprising, since if is far from having orthogonal columns we would expect a lower
ratio.
The explanation is that the constant ratio has been obtained because the size of grows as loses
orthogonality.
(Scaling up the size of any k-dimensional object by a
factor 
increases the ratio by the factor ).
The problem we have is to make the ratio 
as big as possible subject to some limit,
on the tile cross section.
This is because, as we shall show in detail later (and it is clear intuitively), the cross section of a tile
is proportional to the amount of local memory needed to execute it.
The cross section of is also roughly equal to 
.
To satisfy such a bound, we must change the size of .
To keep the problem simple, we shall for the present consider rescaling b by a constant
factor 
. Let be chosen so that
the area of a face, 
, is exactly .
We have that the volume and area of the rescaled tile are
and
Thus, we must choose
We can then achieve the ratio of volume to surface area
On the other hand, if we wish a ratio 
of volume to surface area, we need tiles of
dimension 
. Therefore, we must be able to hold tiles whose sides have area
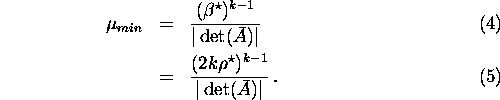
We can, because of these observations, now state the optimality problem we would like to solve:
Given a cone 
, find an integer basis whose elements are in the cone. Choose them so that the
matrix having the scaled basis vectors as columns has largest possible determinant. (We call the determinant
of this scaled matrix the normalized determinant.
This problem is related to, but is not the same as, choosing to minimize its spectral condition number
under the constraints 
.
(See [10] for the definition and properties of matrix condition numbers.)
Consider the vector of singular values of . The normalization
condition places it on the unit sphere in 
. The condition number is the ratio of the largest to the
smallest component; the determinant is the product of the components. In the unconstrained case, both are
optimized by the vector of equal singular values. In the constrained case, however, the optimizing matrices can
differ.
Of course, for general , there may be no maximizer among the integer bases in the cone. And we
do not know whether there is always a maximizing choice when comes from an integer dependence
matrix D.
We can view this problem as the maximization of the real valued function 
over the 
dimensional
space of integer matrices A, subject to m linear inequality constraints 
. It might be fruitful
to use a standard method for the continuous problem and then convert the solution to integer by some rounding-off
procedure; we have not pursued this approach.
In the next section, we consider a heuristic method for choosing the basis A.