




Next: 6.2.6 Summary
Up: Convectively-Dominated Flows and
Previous: 6.2.4 Example Problem
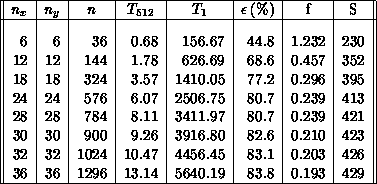
Table 6.1: Timing Results in Seconds for a 512-processor and a
1-processor nCUBE-1. The values 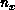 and
and 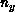 represent the numbers
of grid points per processor in the x and y directions. The
concurrent efficiency, overhead, and speedup are denoted by
represent the numbers
of grid points per processor in the x and y directions. The
concurrent efficiency, overhead, and speedup are denoted by  ,
f, and S.
,
f, and S.
The code was timed for the Kelvin-Helmholtz problem for hypercubes with
dimension ranging from zero to nine. The results for the 512-processor case
are presented in Table 6.1, and show a speedup of 429 for the
largest problem size considered. Subsequently, a group at Sandia National
Laboratories, using a modified version of the code, attained a speedup of
1009 on a 1024-processor nCUBE-1 for a similar type of problem
[Gustafson:88a]. The definitions of concurrent speedup, overhead, and
efficiency are given in Section 3.5.
An analytic model of the performance of the concurrent algorithm was
developed, and ignoring communication latency, the concurrent overhead was
found to be proportional to 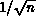 , where n is the number of grid
points per processor. This is in approximate agreement with the results
plotted in Figure 6.3, that shows the concurrent overhead for a
number of different hypercubes dimensions and grain sizes.
, where n is the number of grid
points per processor. This is in approximate agreement with the results
plotted in Figure 6.3, that shows the concurrent overhead for a
number of different hypercubes dimensions and grain sizes.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995

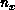 and
and 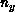 represent the numbers
of grid points per processor in the x and y directions. The
concurrent efficiency, overhead, and speedup are denoted by
represent the numbers
of grid points per processor in the x and y directions. The
concurrent efficiency, overhead, and speedup are denoted by  ,
f, and S.
,
f, and S.




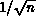 , where n is the number of grid
points per processor. This is in approximate agreement with the results
plotted in Figure
, where n is the number of grid
points per processor. This is in approximate agreement with the results
plotted in Figure