Given a list of existing three-dimensional tracks and a set of observations from a particular sensor, the track extension task nominally consists of three basic steps:
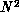operations and
Step 2 requires 
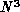. The reduction of the unacceptable polynomial
complexities of Steps 2 and 3 to something approaching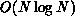 
is
done as follows.
A list of predicted data values for existing tracks is evaluated and is sorted using the same key as was used sorting the data set. The union of the sorted prediction and data sets is then broken into some number of gross subblocks, defined by appropriately large gaps in values of the sorting key. This reduces the single large association problem into a number of smaller subproblems.
For each subproblem, a pruned distance matrix is evaluated, subject to two primary constraints:
where, for i = y,z ,
and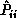 
is the predicted variance for
Equation 18.15 according to the three-dimensional tracking
filter. The score is essentially a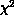 
for the proposed
association, and the cutoff value is typically of order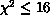 
. The maximum allowed number of associations for any single
prediction is typically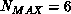 
-8. If more than 
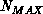data
give acceptable association scores, the possible pairings are sorted by
the association score and only the 
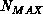best fits (lowest scores)
are kept.
The preceding scoring algorithm leads to a (generally) sparse distance matrix for the large subblocks defined through gaps in the sorting keys. The next step in the algorithm is a quick block diagonalization of the distance matrix through appropriate reorderings of the rows and columns. By this point, the original large association problem has been reduced to a large number of modest sized subproblems and Munkres algorithm for minimizing the global cost in Equation 18.5 is (finally) used to find the optimal pairings.
