




Next: 18.1.2 Asynchronous versus Loosely
Up: 18.1 MetaProblems and MetaSoftware
Previous: 18.1 MetaProblems and MetaSoftware
In this chapter, we discuss some large-scale applications involving a
mixture of several computational tasks. The ISIS system described in
Section 18.2 grew out of several smaller C P projects
undertaken by Rob Clayton and Brad Hager in Caltech's
Geophysics Department. These are described in
[Clayton:87a;88a], [Clayton:88a]
[Gurnis:88a], [Lyzenga:85a;88a],
[Raefsky:88b]. The geophysics applications
in C
P projects
undertaken by Rob Clayton and Brad Hager in Caltech's
Geophysics Department. These are described in
[Clayton:87a;88a], [Clayton:88a]
[Gurnis:88a], [Lyzenga:85a;88a],
[Raefsky:88b]. The geophysics applications
in C P covered a broad range of topics and time scales. At the
longest time scale (
P covered a broad range of topics and time scales. At the
longest time scale (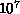 to
to 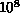 years), Hager's group used
finite-element methods to study thermal convection processes in the
Earth's mantle to understand the dynamics of plate tectonics. A
similar algorithm was used to study the processes involved in
earthquakes and crustal deformation over periods of 10 to 100 years.
On a shorter time scale, Clayton simulated acoustic waves, such as
those generated by an earth tremor in the Los Angeles basin. The
algorithm was finite difference using high-order approximation. This
(synchronous) regular grid was implemented using vector operations as
the basic primitive so that Clayton could easily use both
Cray and hypercube machines. This strategy is a forerunner
of the ideas embodied in the data-parallel High Performance Fortran of
Chapter 13. Tanimoto developed a third type of geophysics
application with the MIMD hypercube decomposed as a pipeline to
calculate the different resonating eigenmodes of the Earth, stimulated
after an earthquake.
years), Hager's group used
finite-element methods to study thermal convection processes in the
Earth's mantle to understand the dynamics of plate tectonics. A
similar algorithm was used to study the processes involved in
earthquakes and crustal deformation over periods of 10 to 100 years.
On a shorter time scale, Clayton simulated acoustic waves, such as
those generated by an earth tremor in the Los Angeles basin. The
algorithm was finite difference using high-order approximation. This
(synchronous) regular grid was implemented using vector operations as
the basic primitive so that Clayton could easily use both
Cray and hypercube machines. This strategy is a forerunner
of the ideas embodied in the data-parallel High Performance Fortran of
Chapter 13. Tanimoto developed a third type of geophysics
application with the MIMD hypercube decomposed as a pipeline to
calculate the different resonating eigenmodes of the Earth, stimulated
after an earthquake.
Sections 18.3 and 18.4 discuss a major
series of simulations that were developed under U. S. Air Force
sponsorship at the Jet Propulsion Laboratory in collaboration with
Caltech. The application is caricatured in
Figure 3.11(b), and Section 18.3 describes
the overall architecture of the simulation. The major module was a
sophisticated parallel Kalman filter and this is
described in Section 18.4. Other complex applications
developed by C P included the use of the Mark IIIfp at JPL in an
image processing system that was used in real
time to analyze images sent down by the space probe Voyager as it sped
past Neptune. One picture produced by the hypercube at
this encounter is shown in Figure 18.1 (Color Plate) [Groom:88a],
[Lee:88a;89b]. Another major data
analysis project in C
P included the use of the Mark IIIfp at JPL in an
image processing system that was used in real
time to analyze images sent down by the space probe Voyager as it sped
past Neptune. One picture produced by the hypercube at
this encounter is shown in Figure 18.1 (Color Plate) [Groom:88a],
[Lee:88a;89b]. Another major data
analysis project in C P involved using the
512-node nCUBE-1 to look at radio astronomy data to uncover the
signature of pulsars. As indicated in
Table 14.3, this system ``discovered'' more pulsars in
1989 than the original analysis software running on a large IBM-3090.
This measure (black holes located per unit time) seems more appropriate
than megaflops for this application. A key algorithm used in the
signal processing was a large, fast Fourier transform that
was hand-coded for the nCUBE. This project also used the concurrent
I/O subsystem on the nCUBE-1 and motivated our initial
software work in this area, which has continued with software support
from ParaSoft Corporation for the Intel Delta machine at Caltech.
Figure 18.2 (Color Plate) illustrates results from this project and
further details will be found in [Anderson:89c;89d;89e;90a],
P involved using the
512-node nCUBE-1 to look at radio astronomy data to uncover the
signature of pulsars. As indicated in
Table 14.3, this system ``discovered'' more pulsars in
1989 than the original analysis software running on a large IBM-3090.
This measure (black holes located per unit time) seems more appropriate
than megaflops for this application. A key algorithm used in the
signal processing was a large, fast Fourier transform that
was hand-coded for the nCUBE. This project also used the concurrent
I/O subsystem on the nCUBE-1 and motivated our initial
software work in this area, which has continued with software support
from ParaSoft Corporation for the Intel Delta machine at Caltech.
Figure 18.2 (Color Plate) illustrates results from this project and
further details will be found in [Anderson:89c;89d;89e;90a],
[Gorham:88a;88d;89a].
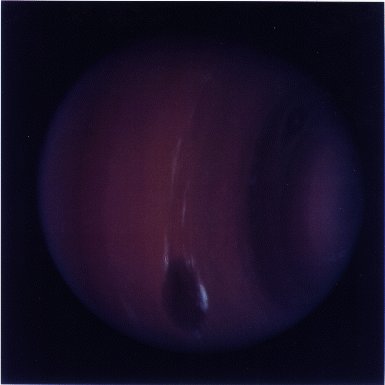
Figure 18.1: Neptune, taken by Voyager 2 in 1989 and
processed by Mark IIIfp.
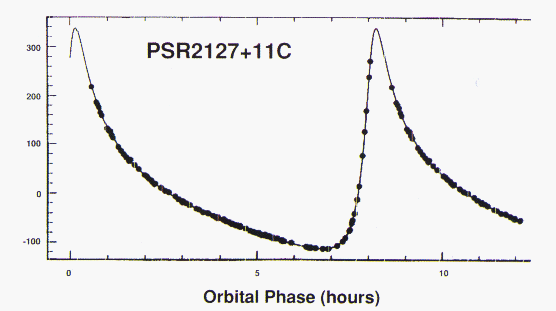
Figure 18.2a: Apparent pluse period of a binary pulsar
in the globular MI5. The approximately eight-hour period (one of the
shortest known) corresponds to high radial velocities that are 0.1% of the
speed of light. This pulsar was discovered from analysis of radio astronomy
data in 1989 by the 512-node nCUBE-1 at Caltech.
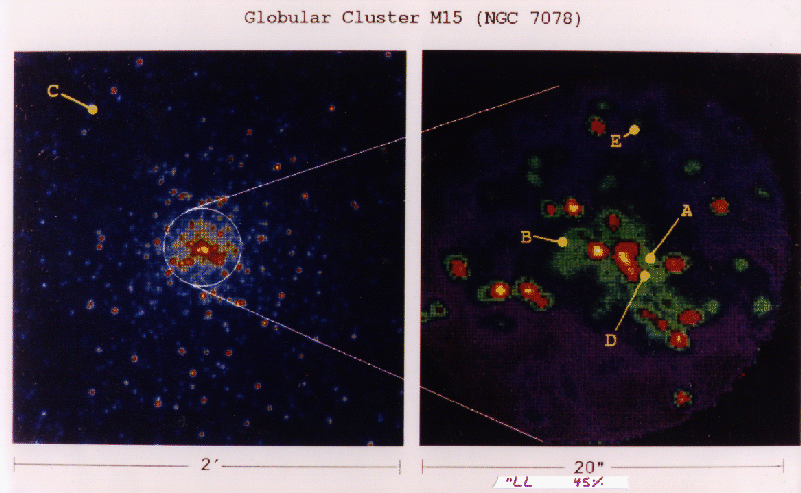
Figure 18.2b: Five pulsares in globular cluster M15.
These were discovered or confirmed (M15 A) by analysis on the nCUBE-1
[Anderson:89d],[Fox:89i;89y;90o],[Gorman:88a].
Another interesting signal-processing application by the same group
was the use of high-performance computing in the removal of
atmospheric disturbance from astronomical images, as illustrated by
Figure 18.3. This combines parallel multidimensional
Fourier transform of the bispectrum with conjugate gradient
[Gorham:88d] minimization to reconstruct the phase. Turbulence,
as shown in Figure 18.3(a), broadens images but one exploits
the approximate constancy of the turbulence due to atmospheric
patches over a 10 to 100 millisecond period. The  Mount Palomar
telescope is used an an interferometer by dividing it spatially onto
one thousand ``separate'' small telescopes. Then standard
astronomical interferometry techniques based on the bispectrum can be
used to remove the turbulence effects, as shown in
Figure 18.3(b), where one has increased statistics by
averaging over 6,000 time slices
[Fox:89i;89n;89y;90o].
Mount Palomar
telescope is used an an interferometer by dividing it spatially onto
one thousand ``separate'' small telescopes. Then standard
astronomical interferometry techniques based on the bispectrum can be
used to remove the turbulence effects, as shown in
Figure 18.3(b), where one has increased statistics by
averaging over 6,000 time slices
[Fox:89i;89n;89y;90o].
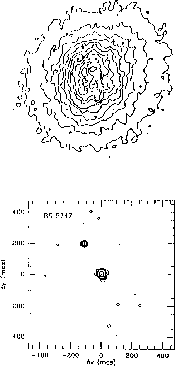
Figure 18.3: Optimal Binary Star Before (a) and After (b) Atmospheric
Turbulence Removed. (a) Raw data from a six second exposure of BS5747
( Corona Borealis) with a diameter of about 1 arcsecond. (b)
The reconstructed image on the nCUBE-1 on the same scale as (a) using
an average over 6,000 frames, each of which lasted 100 milliseconds.
Each figure is magnified by a factor of 1000 over the physical image at
the
Corona Borealis) with a diameter of about 1 arcsecond. (b)
The reconstructed image on the nCUBE-1 on the same scale as (a) using
an average over 6,000 frames, each of which lasted 100 milliseconds.
Each figure is magnified by a factor of 1000 over the physical image at
the 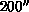 Palomar telescope focus.
Palomar telescope focus.
An important feature of these applications is that they are built up
from a set of modules as exemplified in Figures 3.10,
3.11, 15.1, and 15.2. They fall
into the compound problem class defined in
Section 3.6. We had originally (back in 1989, during a
survey summarized in Section 14.1) classified such metaproblems
as asynchronous. We now realize that metaproblems have a hierarchical
structure-they are an asynchronous collection of modules. However,
this asynchronous structure does not lead to the
parallelization difficulties illustrated by the applications of
Chapter 14. Thus, the ``massive'' parallelism does not come
from the difficult synchronization of the asynchronously linked modules
but rather from internal parallelization of the modules, which are
individually synchronous (as, for example, with the FFT
mentioned above), or loosely synchronous (as in the Kalman Filter of
Section 18.4). One can combine data parallelism inside each
module with the functional asynchronous parallelism by executing each
module concurrently. For example, in the SIM 87, 88, 89 simulations of
Section 18.3, we implemented this with an effective but
crude method. We divided the target machine-a 32-node to 128-node
Mark IIIfp hypercube-into ``subcubes''-that is, the machine was
statically partitioned with each module in Figure 3.11(b)
assigned to a separate partition. Inside each partition, we used a
fast optimized implementation of CrOS, while the parallelism between
partitions was implemented by a variation of the Time Warp mechanism
discussed briefly in Sections 15.3 and 18.3. In the
following subsections, we discuss these software issues more
generally.





Next: 18.1.2 Asynchronous versus Loosely
Up: 18.1 MetaProblems and MetaSoftware
Previous: 18.1 MetaProblems and MetaSoftware
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 P projects
undertaken by Rob Clayton and Brad Hager in Caltech's
Geophysics Department. These are described in
[Clayton:87a;88a], [Clayton:88a]
[Gurnis:88a], [Lyzenga:85a;88a],
[Raefsky:88b]. The geophysics applications
in C
P projects
undertaken by Rob Clayton and Brad Hager in Caltech's
Geophysics Department. These are described in
[Clayton:87a;88a], [Clayton:88a]
[Gurnis:88a], [Lyzenga:85a;88a],
[Raefsky:88b]. The geophysics applications
in C P covered a broad range of topics and time scales. At the
longest time scale (
P covered a broad range of topics and time scales. At the
longest time scale (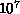 to
to 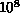 years), Hager's group used
finite-element methods to study thermal convection processes in the
Earth's mantle to understand the dynamics of plate tectonics. A
similar algorithm was used to study the processes involved in
earthquakes and crustal deformation over periods of 10 to 100 years.
On a shorter time scale, Clayton simulated acoustic waves, such as
those generated by an earth tremor in the Los Angeles basin. The
algorithm was finite difference using high-order approximation. This
(synchronous) regular grid was implemented using vector operations as
the basic primitive so that Clayton could easily use both
Cray and hypercube machines. This strategy is a forerunner
of the ideas embodied in the data-parallel High Performance Fortran of
Chapter 13. Tanimoto developed a third type of geophysics
application with the MIMD hypercube decomposed as a pipeline to
calculate the different resonating eigenmodes of the Earth, stimulated
after an earthquake.
years), Hager's group used
finite-element methods to study thermal convection processes in the
Earth's mantle to understand the dynamics of plate tectonics. A
similar algorithm was used to study the processes involved in
earthquakes and crustal deformation over periods of 10 to 100 years.
On a shorter time scale, Clayton simulated acoustic waves, such as
those generated by an earth tremor in the Los Angeles basin. The
algorithm was finite difference using high-order approximation. This
(synchronous) regular grid was implemented using vector operations as
the basic primitive so that Clayton could easily use both
Cray and hypercube machines. This strategy is a forerunner
of the ideas embodied in the data-parallel High Performance Fortran of
Chapter 13. Tanimoto developed a third type of geophysics
application with the MIMD hypercube decomposed as a pipeline to
calculate the different resonating eigenmodes of the Earth, stimulated
after an earthquake.





 P included the use of the Mark IIIfp at JPL in an
image processing
P included the use of the Mark IIIfp at JPL in an
image processing P involved using the
512-node nCUBE-1
P involved using the
512-node nCUBE-1


 Mount Palomar
telescope is used an an interferometer by dividing it spatially onto
one thousand ``separate'' small telescopes. Then standard
astronomical interferometry techniques based on the bispectrum can be
used to remove the turbulence effects, as shown in
Figure
Mount Palomar
telescope is used an an interferometer by dividing it spatially onto
one thousand ``separate'' small telescopes. Then standard
astronomical interferometry techniques based on the bispectrum can be
used to remove the turbulence effects, as shown in
Figure 
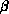 Corona Borealis) with a diameter of about 1 arcsecond. (b)
The reconstructed image on the nCUBE-1 on the same scale as (a) using
an average over 6,000 frames, each of which lasted 100 milliseconds.
Each figure is magnified by a factor of 1000 over the physical image at
the
Corona Borealis) with a diameter of about 1 arcsecond. (b)
The reconstructed image on the nCUBE-1 on the same scale as (a) using
an average over 6,000 frames, each of which lasted 100 milliseconds.
Each figure is magnified by a factor of 1000 over the physical image at
the 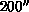 Palomar telescope focus.
Palomar telescope focus.