Speedup is defined as the ratio of sequential running time to parallel running time. We measure the speedup of our program by timing it directly with different numbers of processors on a standard suite of test searches. These searches are done from the even-numbered Bratko-Kopec positions [Bratko:82a], a well-known set of positions for testing chess programs. Our benchmark consists of doing two successive searches from each position and adding up the total search time for all 24 searches. By varying the depth of search, we can control the average search time of each benchmark.
The speedups we measured are shown in Figure 14.8. Each curve corresponds to a different average search time. We find that speedup is a strong function of the time of the search (or equivalently, its depth). This result is a reflection of the fact that deeper search trees have more potential parallelism and hence more speedup. Our main result is that at tournament speed (the uppermost curve of the figure), our program achieves a speedup of 101 out of a possible 256. Not shown in this figure is our later result: a speedup estimated to be 170 on a 512-node machine.
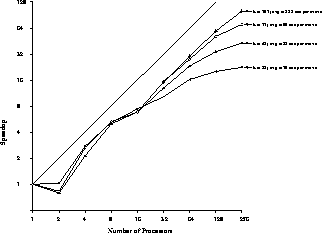
Figure 14.8: The Speedup of the Parallel Chess Program as a Function of
Machine Size and Search Depth. The results are averaged over a
representative test set of 24 chess positions. The speedup increases
dramatically with search depth, corresponding to the fact that there is
more parallelism available in larger searches. The uppermost curve
corresponds to tournament play-the program runs more than 100 times
faster on 256 nodes as on a single nCUBE node when playing at tournament
speed.
The ``double hump'' shape of the curves is also understood: The location of the first dip, at 16 processors, is the location at which the chess tree would like the processor hierarchy to be a one-level hierarchy sometimes, a two-level hierarchy at other times. We always use a one-level hierarchy for 16 processors, so we are suboptimal here. Perhaps this is an indication that a more flexible processor allocation scheme could do somewhat better.