Some good chess programs do run in parallel (see [Finkel:82a], [Marsland:84a], [Newborn:85a], [Schaeffer:84a;86a]), but before our work nobody had tried more than about 15 processors. We were interested in using hundreds or thousands of processors. This forced us to squarely face all the issues of parallel chess-algorithms which work for a few processors do not necessarily scale up to hundreds of processors. An example of this is the occurrence of sequential bottlenecks in the control structure of the program. We have been very careful to keep control of the program decentralized so as to avoid these bottlenecks.
The parallelism comes from searching different parts of the chess tree at the same time. Processors are organized in a hierarchy with one master processor controlling several teams, each submaster controlling several subteams, and so on. The basic parallel operation consists of one master coming to a node in the chess tree, and assigning subtrees to his slaves in a self-scheduled way. Figure 14.5 shows a timeline of how this might happen with three subteams. Self-scheduling by the slaves helps to load-balance the computation, as can be seen in the figure.
So far, we have defined what happens when a master processor reaches a node of the chess tree. Clearly, this process can be repeated recursively. That is, each subteam can split into sub-subteams at some lower level in the tree. This recursive splitting process, illustrated in Figure 14.6, allows large numbers of processors to come into play.
In conflict with this is the inherent sequential model of the standard alpha-beta algorithm. Pruning depends on fully searching one subtree in order to establish bounds (on the score) for the search of the next subtree. If one adheres to the standard algorithm in an overly strict manner, there may be little opportunity for parallelism. On the other hand, if one is too naive in the design of a parallel algorithm, the situation is easily reached where the parallel program searches an impressive number of board positions per second, but still does not search much more deeply than a single processor running the alpha-beta algorithm. The point is that one should not simply split or ``go parallel'' at every opportunity-as we will see below, it is sometimes better to leave processors idle for short periods of time and then do work at more effective points in the chess tree.
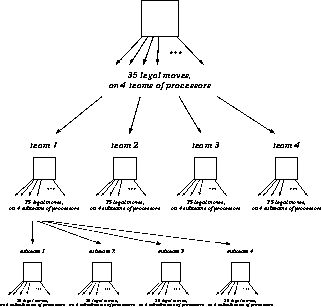
Figure: The Splitting Process of Figure 14.5 is Now
Repeated, in a Recursive Fashion, Down the Chess Tree to Allow Large
Numbers of Processors to Come into Play. The topmost master has four
slaves, which are each in turn an entire team of processors, and so on.
This figure is only approximate, however. As explained in the text, the
splitting into parallel threads of computation is not done at every
opportunity but is tightly controlled by the global hash table.