Coherent Parallel C (CPC) was originally
motivated by the fact that for many parallel algorithms, the Connection
Machine can be very easy to program. The
work of this section is described in [Felten:88a]. Parallel to
our efforts, Philip Hatcher and Michael Quinn have developed a version
of C
, now called Data-Parallel C, for MIMD computers. Their work
is described in [Hatcher:91a].
The CPC language is not simply a C with parallel for loops; instead, a data-parallel programming model is adopted. This means that one has an entire process for each data object. An example of an ``object'' is one mesh point in a finite-element solver. How the processes are actually distributed on a parallel machine is transparent-the user is to imagine that an entire processor is dedicated to each process. This simplifies programming tremendously: complex if statements associated with domain boundaries disappear, and problems which do not exactly match the machine size and irregular boundaries are all handled transparently. Figure 13.17 illustrates CPC by contrasting ``normal'' hypercube programming with CPC programming for a simple grid-update algorithm.
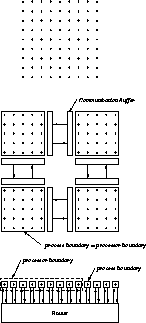
Figure 13.17: Normal Hypercube Programming Model versus CPC Model for the
Canonical Grid-based Problem. The upper part of the figure shows a
two-dimensional grid upon which the variables of the problem live. The
middle portion shows the usual hypercube model for this type of problem.
There is one process per processor and it contains a subgrid. Some variables
of the subgrid are on a process boundary, some are not. Drawn explicitly are
communication buffers and the channels between them which must be managed by
the programmer. The bottom portion of the figure shows the CPC view of the
same problem. There is one data object (a grid point) for each process so
that all variables are on a process boundary. The router provides a full
interconnect between the processes.
The usual communication calls are not seen at all at the user level. Variables of other processes (which may or may not be on another processor) are merely accessed, giving global memory. In our nCUBE implementation, this was implemented using the efficient global communications system called the crystal_router (see Chapter 22 of [Fox:88a]).
An actual run-time system was developed for the nCUBE and is described in [Felten:88a]. Much work remains to be done, of course. How to optimize in order to produce an efficient communications traffic is unexplored; a serious attempt to produce a fine-grained MIMD machine really involves new types of hardware, somewhat like Dally's J-machine.
Ed Felten and Steve Otto developed CPC.