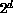This section discusses sorting: the rearrangement of data into some set sequential order. Sorting is a common component of many applications and so it is important to do it well in parallel. Quicksort (to be discussed below) is fundamentally a divide-and-conquer algorithm and the parallel version is closely related to the recursive bisection algorithm discussed in Section 11.1. Here, we have concentrated on the best general-purpose sorting algorithms: bitonic, shellsort, and quicksort. No special properties of the list are exploited. If the list to be sorted has special properties, such as a known distribution (e.g., random numbers with a flat distribution between 0 and 1) or high degeneracy (many redundant items, e.g., text files), then other strategies can be faster. In the case of known data distribution, a bucketsort strategy (e.g., radix sort) is best, while the case of high degeneracy is best handled by the distribution counting method ([Knuth:73a, pp. 379-81]).
The ideas presented here are appropriate for MIMD machines and are somewhat
specific to hypercubes (we will assume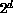 
processors), but can easily be
extended to other topologies.
There are two ways to measure the quality of a concurrent algorithm. The first may be termed ``speed at any cost,'' and here one optimizes for the highest absolute speed possible for a fixed-size problem. The other we can call ``speed per unit cost,'' where one, in addition to speed, worries about efficient use of the parallel machine. It is interesting that in sorting, different algorithms are appropriate depending upon which criterion is employed. If one is interested only in absolute speed, then one should pay for a very large parallel machine and run the bitonic algorithm. This algorithm, however, is inefficient. If efficiency also matters, then one should only buy a much smaller parallel machine and use the much more efficient shellsort or quicksort algorithms.
Another way of saying this is: for a fixed-size parallel computer (the realistic case), quicksort and shellsort are actually the fastest algorithms on all but the smallest problem sizes. We continue to find the misconception that ``Everyone knows that the bitonic algorithm is fastest for sorting.'' This is not true for most combinations of machine size and list size.
The data are assumed to initially reside throughout the parallel computer, spread out in a random, but load-balanced fashion (i.e., each processor begins with an approximately equal number of datums). In our experiments, the data were positive integers and the sorting key was taken to be simply their numeric value. We require that at the end of the sorting process, the data residing in each node are sorted internally and these sublists are also sorted globally across the machine in some way.