




Next: 12.6.7 Summary
Up: 12.6 Cluster Algorithms for
Previous: 12.6.5 Global Equivalencing
The problem of labelling clusters of spins is an example of a standard
graph problem known as connected component labelling
[Horowitz:78a]. Another important instance occurs in image
analysis, in identifying and labelling the connected components of a
binary or multicolored image composed of an array of pixels
[Rosenfeld:82a]. There have been a number of parallel algorithms
implemented for this problem [Alnuweiri:92a] [Cypher:89a],
[Embrechts:89a], [Woo:89a]. The most promising of these
parallel algorithms for spin models has a hierarchical
divide-and-conquer approach [Baillie:91a], [Embrechts:89a].
The processor array is divided up into smaller subarrays of, for
example, 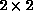 processors. In each subarray, the processors look
at the edges of their neighbors for clusters which are connected across
processor boundaries. As in global equivalencing, these equivalences
are all passed to one of the nodes of the subarray, which places them
in equivalence classes. The results of these partial matchings are
similarly combined on each
processors. In each subarray, the processors look
at the edges of their neighbors for clusters which are connected across
processor boundaries. As in global equivalencing, these equivalences
are all passed to one of the nodes of the subarray, which places them
in equivalence classes. The results of these partial matchings are
similarly combined on each 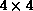 subarray, and this process is
continued until finally all the partial results are merged together on
a single processor to give the global cluster values.
subarray, and this process is
continued until finally all the partial results are merged together on
a single processor to give the global cluster values.
Finally, we should mention the trivial parallelization technique of
running independent Monte Carlo simulations on
different processors. This method works well until the lattice size
gets too big to fit into the memory of each node. In the case of the
Potts model, for example, only lattices of size less than about  or
or 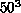 will fit into 1 Mbyte, though most other spin models are more
complicated and more memory-intensive. The smaller lattices which are
seen to give poor speedups in Figure 12.27 and
Figure 12.28 can be run with 100% efficiency in this
way. Note, of course, that this requires an MIMD computer. In fact,
we have used this method to calculate the dynamical critical exponents
of various cluster algorithms for Potts models [Baillie:90m;91b],
[Coddington:92a] (see
Section 4.4.3).
will fit into 1 Mbyte, though most other spin models are more
complicated and more memory-intensive. The smaller lattices which are
seen to give poor speedups in Figure 12.27 and
Figure 12.28 can be run with 100% efficiency in this
way. Note, of course, that this requires an MIMD computer. In fact,
we have used this method to calculate the dynamical critical exponents
of various cluster algorithms for Potts models [Baillie:90m;91b],
[Coddington:92a] (see
Section 4.4.3).





Next: 12.6.7 Summary
Up: 12.6 Cluster Algorithms for
Previous: 12.6.5 Global Equivalencing
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
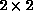 processors. In each subarray, the processors look
at the edges of their neighbors for clusters which are connected across
processor boundaries. As in global equivalencing, these equivalences
are all passed to one of the nodes of the subarray, which places them
in equivalence classes. The results of these partial matchings are
similarly combined on each
processors. In each subarray, the processors look
at the edges of their neighbors for clusters which are connected across
processor boundaries. As in global equivalencing, these equivalences
are all passed to one of the nodes of the subarray, which places them
in equivalence classes. The results of these partial matchings are
similarly combined on each 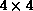 subarray, and this process is
continued until finally all the partial results are merged together on
a single processor to give the global cluster values.
subarray, and this process is
continued until finally all the partial results are merged together on
a single processor to give the global cluster values.





 or
or 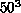 will fit into 1 Mbyte, though most other spin models are more
complicated and more memory-intensive. The smaller lattices which are
seen to give poor speedups in Figure
will fit into 1 Mbyte, though most other spin models are more
complicated and more memory-intensive. The smaller lattices which are
seen to give poor speedups in Figure