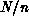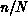The efficiency of any parallel algorithm increases as the computational
load dominates the communication load [Williams:90a]. In the case
of a domain-decomposed mesh, the computational time depends on the
number of elements per processor, and the communication time on the
number of nodes at the boundary of the processor domain. If there are
N elements in total, distributed among n processors, we expect the
computation to go as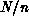 
and the communication as the square root of
this, so that the efficiency should approach unity as the square root
of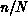 
.
We have run the example described above starting with a mesh of 525 elements, and refining 50% of the elements. In fact, more than 50% will be refined because of the nature of the refinement algorithm:In practice, it is about 70%. The refinement continues until the memory of the machine runs out.
Figure 12.9 shows timing results. At top right are results for
1, 4, 16, 64, and 256 nCUBE processors. The time taken per simulation
time step is shown for the compressible flow algorithm against number of
elements in the simulation. The curves end when the processor memory is
full. Each processor offers a nominal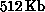 
memory, but when all the
software and communication buffers are accounted for, there is only about
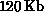available for the mesh.
The top left of Figure 12.9 shows the same curves for 1, 4, 16, 64, and 128 Symult processors, and at bottom left the results for 1, 4, 16, and 32 processors of a Meiko CS-1 computing surface. For comparison, the bottom right shows the results for one head of the CRAY Y-MP, and also for the Sun Sparcstation.
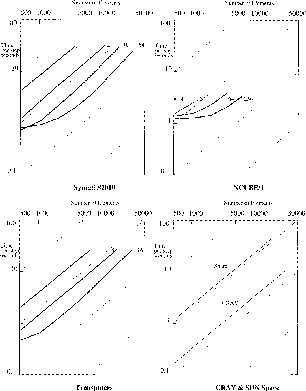
Figure 12.9: Timings for Transonic Flow
Each figure has diagonal lines to guide the eye; these are lines of constant time per element. We expect the curves for the sequential machines to be parallel to these because the code is completely local and the time should be proportional to the number of elements. For the parallel machines, we expect the discrepancy from parallel lines to indicate the importance of communication inefficiency.