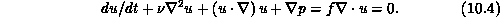
We have implemented a sophisticated incompressible flow solver using DIME and DIMEFEM. The algorithm is described more completely in [Bristeau:87a]. The evolution equation for an incompressible Newtonian fluid of viscosity n is
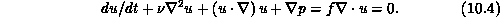
We use a three-stage operator-split scheme whereby for each time step of length dt, the equation is integrated
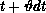with incompressibility and no convection,
then
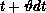to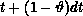 
with convection and
no incompressibility condition, then
The parameter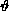 
is 
.
Each of these three implicit steps involves the solution of either a Stokes problem:
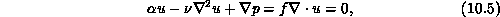
or the nonlinear problem:\
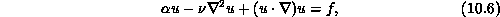
where 
is a parameter inversely proportional to the time step. We
solve the Navier-Stokes equation, and
consequently also these subsidiary problems, with given velocity at the
boundary (Dirichlet boundary conditions).