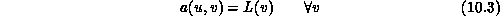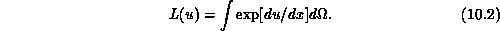





Finite-element approximations to functions form a finite-dimensional vector space, and as such may be multiplied by a scalar and added. Functions are provided to do these operations. If the function is expressed as Lagrangian elements it may also be differentiated, which changes the order of representation: For example, differentiating a quadratic element produces a linear element.
At present, DIMEFEM provides two kinds of elements, Lagrangian and Gaussian, although strictly speaking the latter is not a finite element because it possesses no interpolation functions. The Gaussian element is simply a collection of function values at points within each triangle and a set of weights, so that integrals may be done by summing the function values multiplied by the weights. As with one-dimensional Gaussian integration, integrals are exact to some polynomial order. We cannot differentiate Gaussian FEFs, but can apply pointwise operators such as multiplication and function evaluation that cannot be done in the Lagrangian representation.
Consider the nonlinear operator L defined by
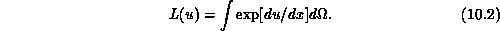
The most accurate way to evaluate this is to start with u in Lagrangian form, differentiate, convert to Gaussian representation, exponentiate, then multiply by the weights and sum. This can be done explicitly with DIMEFEM, but in the future we hope to create an environment which ``knows'' about representations, linearity, and so on, and can parse an expression such as the above and evaluate it correctly.
The computational kernel of any finite-element software is the linear solver. We have implemented this with preconditioned conjugate gradient , so that the user supplies a linear operator L, an elliptic bilinear operator a, a scalar product S (a strongly elliptic symmetric bilinear operator which satisfies the triangle inequality), and an initial guess for the solution. The conjugate-gradient solver replaces the guess by the solution u of the standard variational equation