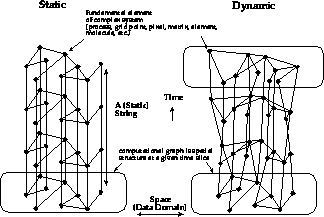
Figure 3.7: (a) Synchronous, Loosely Synchronous (Static), and (b) Asynchronous (Dynamic) Complex Systems with their Space-Time Structure





In the previous section, we showed how the process of computation could be viewed as mappings between complex systems. As the book progresses, we will quantify this by providing examples that cover a range of problem architectures. In the next three sections, we will set up the general framework and define terms which will be made clearer later on as we see the explicit problems with their different architectures. The concept of complex systems may have very general applicability to a wide range of fields but here we will focus solely on their application to computation. Thus, our discussion of their properties will only cover what we have found useful for the task at hand. These properties are surely more generally applicable, and one can expect that other ideas will be needed in a general discussion. Section 3.3 gives examples and a basic definition of a complex system and its associated space-time structure. Section 3.4 defines temporal properties and, finally, Section 3.5 spatial structures.
We wish to understand the interesting characteristics or structure of a complex system. We first introduce the concept of space-time into a general complex system. As shown in Figure 3.7, we consider a general complex system as a space, or data domain, that evolves deterministically or probabilistically with time. Often, the space-time associated with a given complex system is identical with physical space-time but sometimes it is not. Let us give some examples.

Figure 3.7: (a) Synchronous, Loosely Synchronous (Static), and (b)
Asynchronous (Dynamic) Complex Systems with their Space-Time Structure
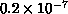 seconds
for a
seconds
for a 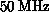 node.
node.
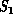 ) which is first mapped, by the theoretical
geophysicist who is modelling it, into displacements measured by the
amplitudes of waves as a function of space and time. Here again, the
complex system (
) which is first mapped, by the theoretical
geophysicist who is modelling it, into displacements measured by the
amplitudes of waves as a function of space and time. Here again, the
complex system ( ) space-time is mapped into physical
space-time. One might Fourier-Transform this picture to obtain a third
complex system (
) space-time is mapped into physical
space-time. One might Fourier-Transform this picture to obtain a third
complex system ( ) whose space is now labelled by wave numbers.
) whose space is now labelled by wave numbers.
 ) is a collection of N
sheets of paper. The space of
) is a collection of N
sheets of paper. The space of  consists of the set of sheets and has
N discrete members. The time associated with
consists of the set of sheets and has
N discrete members. The time associated with 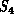 is the
extension along the ``long'' (say x) direction of each sheet. This complex
system is specified by the recording on the other (y) direction as a
function of the time defined above. This example illustrates how
mappings between complex systems can mix space and time. This is further
illustrated by the next example, which completes the sequence of complex
systems related to earthquakes.
is the
extension along the ``long'' (say x) direction of each sheet. This complex
system is specified by the recording on the other (y) direction as a
function of the time defined above. This example illustrates how
mappings between complex systems can mix space and time. This is further
illustrated by the next example, which completes the sequence of complex
systems related to earthquakes.
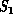 into one
(
into one
(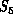 ) with perhaps one or at best a few elements in its spatial domain
corresponding to the independent functional units on the workstation.
) with perhaps one or at best a few elements in its spatial domain
corresponding to the independent functional units on the workstation. 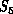 has mapped the original space-time into a totally temporal complex
system. This could be viewed either as an example of the richness of mappings
allowed between complex systems or as an illustration of the artificial nature
of the sequential computing! Simulation of an earthquake on a parallel
computer more faithfully links the space-time of the problem (
has mapped the original space-time into a totally temporal complex
system. This could be viewed either as an example of the richness of mappings
allowed between complex systems or as an illustration of the artificial nature
of the sequential computing! Simulation of an earthquake on a parallel
computer more faithfully links the space-time of the problem (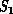 ) with that
of the simulation (
) with that
of the simulation (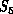 ).
).
Consider instead the solution of the elliptic partial differential equation
for the electrostatic potential 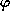 in the presence of a charge density
in the presence of a charge density
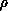 . A simple, albeit usually non-optimal approach to solving
Equation 3.4, is a Jacobi iteration, which in the special case
of two dimensions and
. A simple, albeit usually non-optimal approach to solving
Equation 3.4, is a Jacobi iteration, which in the special case
of two dimensions and 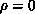 involves the iterative procedure
involves the iterative procedure
where we assume that integer values of the indices x and y label the
two-dimensional grid on which Laplace's equation is to
be solved. The complex system defined by Equation 3.5
has spatial domain defined by the 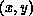 grid and a temporal dimension defined by the iteration index n. Indeed, the
Jacobi iteration is mathematically related to solving the parabolic
partial differential equation
grid and a temporal dimension defined by the iteration index n. Indeed, the
Jacobi iteration is mathematically related to solving the parabolic
partial differential equation
where one relates the discretized time t to the iteration index n. This
equivalence between Equations 3.5 and 3.6
is qualitatively preserved when one compares the solution of
Equations 3.3 and 3.5. As long as one
views iteration as a temporal structure,
Equations 3.3 and 3.4 can be formulated
numerically with isomorphic complex systems 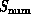 . This implies
that parallelization issues, both hardware and software, are
essentially identical for both equations.
. This implies
that parallelization issues, both hardware and software, are
essentially identical for both equations.
The above example illustrates the most important form of
parallelism-namely, data parallelism. This is produced by
parallel execution of a computational (temporal) algorithm on each
member of a space or data domain. Data parallelism is
essentially synonymous with either massive parallelism or massive data parallelism. Spatial domains are usually very large,
with from 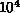 to
to 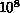 members today; thus exploiting this data
parallelism does lead to massive parallelism.
members today; thus exploiting this data
parallelism does lead to massive parallelism.
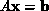 with a dense (few zero
elements) matrix A.
with a dense (few zero
elements) matrix A.
Parallelization of this is covered fully in [Fox:88a] and
Chapter 8 of this book. Gaussian elimination (LU decomposition)
for solving Equation 3.7 involves successive steps where
in the simplest formulation without pivoting, at step
k one ``eliminates'' a single variable 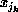 where the index
where the index 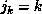 . At each step k, one modifies both
. At each step k, one modifies both 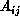 and
and 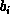
and 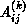 ,
, 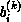 are formed from
are formed from 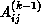 ,
,
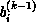
where one ensures (if no pivoting is employed) that
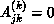 when j>k. Consider the above procedure as a
complex system. The spatial domain is formed by the matrix A
with a two-dimensional array of values
when j>k. Consider the above procedure as a
complex system. The spatial domain is formed by the matrix A
with a two-dimensional array of values 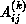 . The time domain
is labelled by the index k and so is a discrete space with n
(number of rows or columns of A) members. The space is also discrete
with
. The time domain
is labelled by the index k and so is a discrete space with n
(number of rows or columns of A) members. The space is also discrete
with 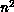 members.
members.




