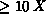Neural nets are ``by definition'' parallel computing systems of many densely interconnected units. Parallel computation is the basic method used by our brain to achieve response times of hundreds of milliseconds, using sloppy biological hardware with computing times of a few milliseconds per basic operation.
Our implementation of the learning algorithm is based on the use of MIMD
machines with large grain size. An efficient mapping strategy consists of
assigning a subset of the examples (input-output pairs) and the
entire network structure to each processor. To obtain proper
generalization, the number of example patterns has to be much larger (say,
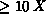) than the number of parameters defining the architecture
(i.e., the number of connection weights). For this reason, the amount
of memory used for storing the weights is not too large for significant
problems.
Function and gradient evaluation is executed in parallel. Each processor calculates the contribution of the assigned patterns (with no communication), and a global combining-distributing step (see the ADDVEC routine in [Fox:88a]) calculates the total energy and gradient (let's remember that the energy is a sum of the patterns' contributions) and communicates the result to all processors.
Then the one-dimensional minimization along the search direction is completed and the weights are updated.
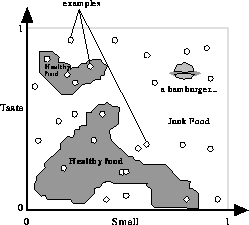
Figure 9.25: ``Healthy Food'' Has to Be Distinguished from ``Junk Food'' Using
Taste and Smell Information.
This simple parallelization approach is promising: It can be easily adapted to
different network representations and learning strategies, and it is going to
be a fierce competitor with analog implementations of neural networks, when
these are available for significant applications (let's remember that
airplanes do not flap their wings 
).