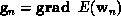 ,
, 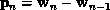 and
and
 . The one-dimensional search
direction for the nth iteration is a modification of the gradient
. The one-dimensional search
direction for the nth iteration is a modification of the gradient
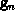 , as follows:
, as follows:





Steepest descent suffers from a bad reputation with researchers in optimization. From the literature (e.g., [Gill:81a]), we found a wide selection of more appropriate optimization techniques. Following the ``decision tree'' and considering the characteristics of large supervised learning problems (large memory requirements and time-consuming calculations of the energy and the gradient), the Broyden-Fletcher-Goldfarb-Shanno one-step memoryless quasi-Newton method (all adjectives are necessary to define it) is a good candidate in the competition and performed very efficiently on different problems.
Let's define the following vectors: 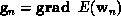 ,
, 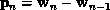 and
and
 . The one-dimensional search
direction for the nth iteration is a modification of the gradient
. The one-dimensional search
direction for the nth iteration is a modification of the gradient
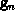 , as follows:
, as follows:
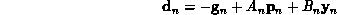
Every N steps (N being the number of weights in the network), the search is restarted in the direction of the negative gradient.
The coefficients 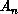 and
and 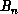 are combinations of scalar products:
are combinations of scalar products:
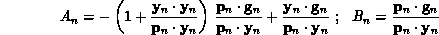
The one-dimensional minimization used in this work is based on quadratic interpolation and tuned to back-propagation where, in a single step, both the energy value and the negative gradient can be efficiently obtained. Details on this step are contained in [Williams:87b].
The computation during each step requires 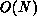 operations (the same
behavior as standard batch back-propagation), while the CPU time for
each step increases by an average factor of three for the problems
considered. Because the total number of steps for
convergence is much smaller, we measured a large net
benefit in computing time.
operations (the same
behavior as standard batch back-propagation), while the CPU time for
each step increases by an average factor of three for the problems
considered. Because the total number of steps for
convergence is much smaller, we measured a large net
benefit in computing time.
Last but not least, this method can be efficiently implemented on MIMD parallel computers.