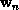The multilayer perceptron, initialized with random weights, presents random output patterns. We would like to execute a learning stage, progressively modifying the values of the connection strengths in order to make the outputs nearer to the prescribed ones.
It is straightforward to transform the learning task into an optimization problem (i.e., a search for the minimum of a specified function, henceforth called energy). If the energy is defined as the sum of the squared errors between obtained and desired output pattern over the set of examples, minimizing it will accomplish the task.
A large fraction of the theoretical and applied research in supervised
learning is based on the steepest descent method for minimization.
The negative gradient of the energy with respect to the weights is
calculated during each iteration, and a step is taken in that direction (if
the step is small enough, energy reduction is assured). In this way, one
obtains a sequence of weight vectors,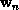 
, that converges to a
local minimum of the energy function:
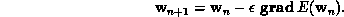
Now, given that we are interested in converging to the local minimum in the
shortest time (this is not always the case: to combat noise some slowness may
be desired), there is no good reason to restrict ourselves to steepest
descent, and there are at least a couple of reasons in favor of other
methods. First, the learning speed, 
, is a free
parameter that has to be chosen carefully for each problem (if it is too
small, progress is slow; if too large, oscillations may be created).
Second, even in the optimal case of a step along the steepest descent
direction bringing the system to the absolute minimum (along this
direction), it can be proved that steepest descent can be arbitrarily slow,
particularly when ``the search space contains long ravines that are
characterized by sharp curvature across the ravine and a gently sloping
floor'' [Rumelhart:86b]. In other words, if we are unlucky with the
choice of units along the different dimensions (and this is a frequent event
when the number of weights is 1000 or 10,000), it may be the case that during
each iteration, the previous error is reduced by 0.000000001%!
The problem is essentially caused by the fact that the gradient does not necessarily point in the direction of the minimum, as it is shown in Figure 9.23.
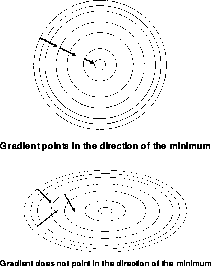
Figure 9.23: Gradient Direction for Different Choice of Units
If the energy is quadratic, a large ratio of the maximum to minimum eigenvalues causes the ``zigzagging'' motion illustrated. In the next sections, we will illustrate two suggestions for tuning parameters in an adaptive way and selecting better descent directions.