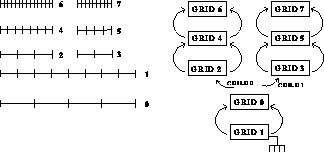
Figure 9.16: One-Dimensional Adaptive Multigrid Structure





Here, we focus on the use of adaptive grids for sequential computations. We shall apply these ideas in the next section to achieve concurrency. Figure 9.16 illustrates the grid structure of a one-dimensional adaptive multigrid procedure. Fine grids are introduced only where necessary, in the neighborhood of a singularity, for example. In two and three dimensions the topology is more complicated, and it makes sense to refine in several subdomains that partially overlap.

Figure 9.16: One-Dimensional Adaptive Multigrid Structure
We focus first on the intergrid transfers. Although these operators are straightforward, they are the source of some implementation difficulties for the concurrent algorithm, because load-balanced data distributions of fine and coarse grids are not compatible. The structure introduced here avoids these difficulties. Before introducing a fine grid on a subdomain, we construct an artificial coarse grid on the same subdomain. This artificial coarse grid, called a child grid, differs from a normal grid data structure only because its data vectors (the solution and right-hand side) are subvectors of the parent-grid data vectors. Thus, child grids do not use extra memory for data (except for some negligible amount for bookkeeping). In Figure 9.16, grid 1 is a parent-grid with two children, grids 2 and 3. With child grids, the intergrid transfers of the nonadaptive procedure can be reused. The restriction, for example, takes place between a fine grid (defined over a subdomain) and a coarse child grid (in Figure 9.16, between grids 4 and 2 and between grids 5 and 3, respectively). Because data memory of child and parent grid are shared, the appropriate subvectors of the coarse grid data are updated automatically. Similarly, prolongation occurs between the child grid and the fine grid.
The basic data structure of the nonadaptive procedure, the doubly linked list of grids, is transformed radically as a result of child grids and their refinements. The data structure is now a tree of doubly linked lists; see Figure 9.16. As mentioned before, the intergrid transfers are not affected by this complicated structure. For relaxation, the only significant difference is that more than one grid may have to be relaxed on each level. When the boundary of one grid intersects the interior of another grid on the same level, the boundary values must be interpolated (Figure 9.17). This does not affect the relaxation operators, as long as the relaxation step is preceded by a boundary-interpolation step.
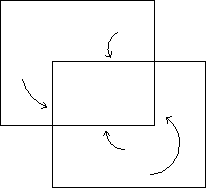
Figure 9.17: Boundary Interpolation




