




Next: 9.6.6 Conclusions
Up: Concurrent DASSL Applied
Previous: Residual Communication
The algorithms and formalism needed to run this example amount to about
70,000 lines of C code including the simulation layer, Concurrent DASSL,
the linear algebra packages, and support functions [Skjellum:90a;90c;90d].
In this simulation, we consider seven distillation columns arranged in a tree sequence [Skjellum:90c], working on the
distillation of eight alcohols: methanol, ethanol, propan-1-ol,
propan-2-ol, butan-1-ol, 2-methyl propan-1-ol, butan-2-ol, and 2-methyl
propan-2-ol. Each column has 143 trays. Each tray is initialized to a
nonsteady condition, and the system is relaxed to the steady state
governed by a single-feed stream to the first column in the sequence.
This setup generates suitable dynamic activity for illustrating the
cost of a single ``transient'' integration step.
We note the performance in Table 9.6. Because we have not
exploited latency in the Jacobian computation, this calculation is quite
expensive, as seen for the sequential times on a Sun 3/260 depicted there.
(The timing for the Sun 3/260 is quite comparable to a single Symult s2010
node and was lightly loaded during this test run.) As expected, Jacobian
calculations speed up efficiently, and we are able to get an approximate
speedup of 100 for this step using 128 nodes. The A-mode linear algebra also
speeds up significantly. The B-mode factorization speeds up negligibly and
quickly slows down again for more than 16 nodes. Likewise, the triangular
solves are significantly slower than the sequential time. It should be noted
that B-mode reflects two orders of magnitude speed improvement over A-mode.
This reflects the fact that we are seeing almost linear time complexity in
B-mode, since this example has a narrow block tridiagonal Jacobian with too
little off-diagonal coupling to generate much fill-in. It seems hard to
imagine speeding up B-mode for such an example, unless we can exploit
multiple pivots. We expect multiple-pivot heuristics to do reasonably well
for this case, because of its narrow structure, and nearly block tridiagonal
structure. We have used Wilson Equation Vapor-Liquid Equilibrium with the
Antoine Vapor equation. We have found that the thermodynamic calculations
were much less demanding than we expected, with bubble-point computations
requiring ``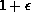 '' iterations to converge. Consequently, there was
not the greater weight of Jacobian calculations we expected beforehand. Our
model assumes constant pressure, and no enthalpy balances. We include no
flow dynamics and include liquid and vapor flows as states, because of the
possibility of feedbacks.
'' iterations to converge. Consequently, there was
not the greater weight of Jacobian calculations we expected beforehand. Our
model assumes constant pressure, and no enthalpy balances. We include no
flow dynamics and include liquid and vapor flows as states, because of the
possibility of feedbacks.
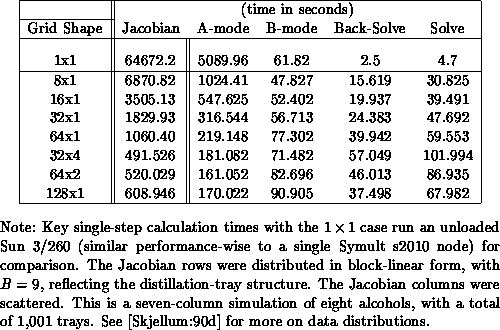
Table 9.6: Order 9009 Dynamic Simulation Data
If we utilize latency in the Jacobian calculation, we
could reduce the sequential time by a factor of about 100. This
improvement would also carry through to the concurrent times for
Jacobian solution. At that ratio, Jacobian computation to B-mode
factorization has a sequential ratio of about 10:1. As is, we achieve
legitimate speedups of about five. We expect to improve these results
using the ideas quoted elsewhere in this book and in
[Skjellum:90d].
From a modelling point-of-view, two things are important to note.
First, the introduction of more nonideal thermodynamics would improve
speedup, because these calculations fall within the Jacobian
computation phase and single-residual computation. Furthermore, the
introduction of a more realistic model will likewise bear on
concurrency, and likely improve it. For example, introducing flow
dynamics, enthalpy balances, and vapor holdups makes the model more
difficult to solve numerically (higher index). It also increases the
chance for a wide range of stepsizes, and the possible need for
additional A-mode factorizations to maintain stability in the
integration process. Such operations are more costly, but also have a
higher speedup. Furthermore, the more complex models will be less
likely to have near diagonal dominance; consequently more
pivoting is to be expected, again increasing the
chance for overall speedup compared to the sequential case. Mainly, we
plan to consider the waveform-relaxation
approach more heavily, and also to consider new classes of dynamic
distillation simulations with Concurrent DASSL [Skjellum:90c].





Next: 9.6.6 Conclusions
Up: Concurrent DASSL Applied
Previous: Residual Communication
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
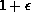 '' iterations to converge. Consequently, there was
not the greater weight of Jacobian calculations we expected beforehand. Our
model assumes constant pressure, and no enthalpy balances. We include no
flow dynamics and include liquid and vapor flows as states, because of the
possibility of feedbacks.
'' iterations to converge. Consequently, there was
not the greater weight of Jacobian calculations we expected beforehand. Our
model assumes constant pressure, and no enthalpy balances. We include no
flow dynamics and include liquid and vapor flows as states, because of the
possibility of feedbacks.





