




Next: Studies of Electron-Molecule
Up: Quantum Mechanical Reactive
Previous: 8.2.3 Parallel Algorithm
Accuracy
Calculations were performed for the 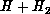 system on the LSTH
surface [Liu:73a], [Siegbahn:78a],
[Truhlar:78a;79a] for partial waves with total
angular momentum J = 0,1,2 and energies up to
system on the LSTH
surface [Liu:73a], [Siegbahn:78a],
[Truhlar:78a;79a] for partial waves with total
angular momentum J = 0,1,2 and energies up to 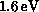 . Flux is
conserved to better than 1% for J = 0, 2.3% for J = 1, and 3.6%
for J = 2 for all open channels over the entire energy range considered.
. Flux is
conserved to better than 1% for J = 0, 2.3% for J = 1, and 3.6%
for J = 2 for all open channels over the entire energy range considered.
To illustrate the accuracy of the 32-bit arithmetic calculations, the
scattering results from the Mark IIIfp with 64 processors are shown in
Figure 8.7 for J = 0, in which some transition probabilities
as a function of the total collision energy, E, are plotted. The
differences between these results, and those obtained using a CRAY X-MP/48
and a CRAY-2, do not exceed 0.004 in absolute value over the energy range
investigated.
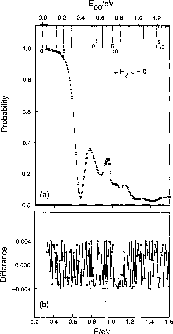
Figure 8.7: Probabilities as a Function of Total Energy E (Lower Abscissa)
and Initial Relative Translational Energy  (Upper Abscissa) for the
(Upper Abscissa) for the
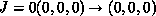
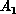 Symmetry Transition in
Symmetry Transition in
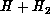 Collisions on the LSTH Potential Energy Surface. The symbol
Collisions on the LSTH Potential Energy Surface. The symbol
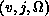 labels an asymptotic state of the
labels an asymptotic state of the 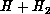 system in which
v, j, and
system in which
v, j, and 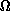 are the quantum numbers of the initial or final
are the quantum numbers of the initial or final 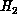 states. The vertical arrows on the upper abscissa denote the energies at
which the corresponding
states. The vertical arrows on the upper abscissa denote the energies at
which the corresponding 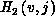 states open up. The length of those
arrows decreases as v spans the values 0, 1, and 2, and the numbers 0, 5,
and 10 associated with the arrows define a labelling for the value of j.
The number of LHSF used was 36 and the number of primitives used to calculate
these surface functions was 80.
states open up. The length of those
arrows decreases as v spans the values 0, 1, and 2, and the numbers 0, 5,
and 10 associated with the arrows define a labelling for the value of j.
The number of LHSF used was 36 and the number of primitives used to calculate
these surface functions was 80.
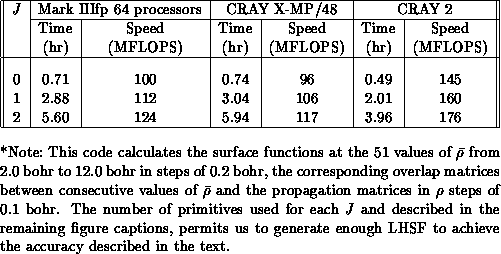
Table 8.3: Performance of the surface function code.*
Timing and Parallel Efficiency
In Tables 8.3 and 8.4, we present the
timing data on the 64-processor Mark IIIfp, a CRAY X-MP/48 and a CRAY 2, for
both the surface function code (including calculation of the overlap
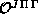 and interaction
and interaction 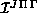 matrices) and the logarithmic derivative propagation code. For the surface
function code, the speeds on the first two machines are about the same.
The CRAY 2 is 1.43 times faster than the Mark IIIfp and 1.51 times faster
than the CRAY X-MP/48 for this code. The reason is that this program is
dominated by matrix-vector multiplications which are done in optimized
assembly code in all three machines. For this particular operation, the
CRAY 2 is 2.03 times faster than the CRAY X-MP/48 whereas, for more
memory-intensive operations, the CRAY 2 is slower than the CRAY X-MP/48
[Pfeiffer:90a]. A slightly larger primitive basis set is required on
the Mark IIIfp in order to obtain surface function energies of an accuracy
equivalent to that obtained with the CRAY machines. This is due to the lower
accuracy of the 32-bit arithmetic of the former with respect to the 64-bit
arithmetic of the latter.
matrices) and the logarithmic derivative propagation code. For the surface
function code, the speeds on the first two machines are about the same.
The CRAY 2 is 1.43 times faster than the Mark IIIfp and 1.51 times faster
than the CRAY X-MP/48 for this code. The reason is that this program is
dominated by matrix-vector multiplications which are done in optimized
assembly code in all three machines. For this particular operation, the
CRAY 2 is 2.03 times faster than the CRAY X-MP/48 whereas, for more
memory-intensive operations, the CRAY 2 is slower than the CRAY X-MP/48
[Pfeiffer:90a]. A slightly larger primitive basis set is required on
the Mark IIIfp in order to obtain surface function energies of an accuracy
equivalent to that obtained with the CRAY machines. This is due to the lower
accuracy of the 32-bit arithmetic of the former with respect to the 64-bit
arithmetic of the latter.
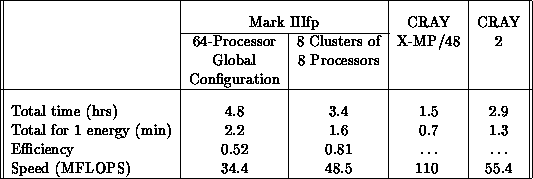
Table 8.4: Performance of the logarithmic derivative code. Based on a
calculation using 245 surface functions and 131 energies, and a
logarithmic derivative integration step of 0.01 bohr.
The efficiency ( ) of the parallel LHSF code was determined
using the definition
) of the parallel LHSF code was determined
using the definition 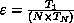 , where
, where
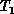 and
and 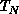 are, respectively, the implementation times using a
single-processor and N processors. The single processor times are
obtained from runs performed after removing the overhead of the
parallel code, that is, after removing the communication calls and some
logical statements. Perfect efficiency (
are, respectively, the implementation times using a
single-processor and N processors. The single processor times are
obtained from runs performed after removing the overhead of the
parallel code, that is, after removing the communication calls and some
logical statements. Perfect efficiency ( ) implies
that the N-processor hypercube is N times faster than a single
processor. In Figure 8.8, efficiencies for the surface
function code (including the calculation of the overlap and interaction
matrices) as a function of the size of the primitive basis set are
plotted for 2, 4, 8, 16, 32 and 64 processor configurations of the
hypercube. The global dimensions of the matrices used are chosen to be
integer multiples of the number of processor rows and columns in order
to insure load balancing among the processors. Because of the limited
size of a single-processor memory, the efficiency determination is
limited to 32 primitives. As shown in Figure 8.8, the
efficiencies increase monotonically and approach unity asymptotically
as the size of the calculation increases. Converged results require
large enough primitive basis sets so that the efficiency of the surface
function code is estimated to be about 0.95 or greater.
) implies
that the N-processor hypercube is N times faster than a single
processor. In Figure 8.8, efficiencies for the surface
function code (including the calculation of the overlap and interaction
matrices) as a function of the size of the primitive basis set are
plotted for 2, 4, 8, 16, 32 and 64 processor configurations of the
hypercube. The global dimensions of the matrices used are chosen to be
integer multiples of the number of processor rows and columns in order
to insure load balancing among the processors. Because of the limited
size of a single-processor memory, the efficiency determination is
limited to 32 primitives. As shown in Figure 8.8, the
efficiencies increase monotonically and approach unity asymptotically
as the size of the calculation increases. Converged results require
large enough primitive basis sets so that the efficiency of the surface
function code is estimated to be about 0.95 or greater.
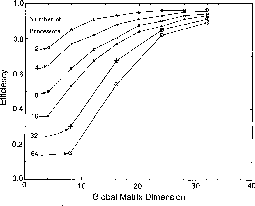
Figure 8.8: Efficiency of the Surface Function Code (Including the Calculation
of the Overlap and Interaction Matrices) as a Function of the Global Matrix
Dimension (i.e., the Size of the Primitive Basis Set) for 2, 4, 8, 16,
32, and 64 Processors. The solid curves are straight line segments
connecting the data points for a fixed number of processors and are provided
as an aid to examine the trends.
The data for the logarithmic derivative code given in
Table 8.4 for a 245-channel (i.e., LHSF) example show
that the Mark IIIfp has a speed about 62% of that of the CRAY 2, but
only about 31% of that of the CRAY X-MP/48. This code is dominated by
matrix inversions, which are done in optimized assembly code in all
three machines. The reason for the slowness of the hypercube with
respect to the CRAYs is that the efficiency of the parallel logarithmic
derivative code is 0.52. This relatively low value is due to the fact
that matrix inversions require a significant amount of interprocessor
communication. Figure 8.9 displays efficiencies of the
logarithmic derivative code as a function of the number of channels
propagated for different processor configurations, as done previously
for the Mark III [Hipes:88b], [Messina:90a] hypercubes. The
data can be described well by an operations count formula developed
previously for the matrix inversion part of the code
[Hipes:88a]; this formula can be used to extrapolate the data to
larger numbers of processors or channels. It can be seen that for an
8-processor configuration, the code runs with an efficiency of 0.81.
This observation suggested that we divide the Mark IIIfp into eight
clusters of eight processors each, and perform calculations for
different energies in different clusters. The corresponding timing
information is also given in Table 8.4. As can be seen
from the last row of this table, the speed of the logarithmic
derivative code using this configuration of the 64-processor Mark IIIfp
is 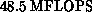 , which is about 44% of that of the CRAY X-MP/48
and 88% of that of the CRAY 2. As the number of channels increases,
the number of processors per cluster may be made larger in order to
increase the amount of memory available in each cluster. The
corresponding efficiency should continue to be adequate due to the
larger matrix dimensions involved.
, which is about 44% of that of the CRAY X-MP/48
and 88% of that of the CRAY 2. As the number of channels increases,
the number of processors per cluster may be made larger in order to
increase the amount of memory available in each cluster. The
corresponding efficiency should continue to be adequate due to the
larger matrix dimensions involved.
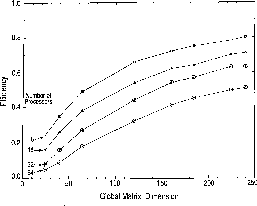
Figure 8.9: Efficiency of Logarithmic Derivative Code as a Function of the
Global Matrix Dimension (i.e., the Number of Channels or LHSF) for 8,
16, 32, and 64 Processors. The solid curves are straight-line segments
connecting the data points for a fixed number of processors, and are provided
as an aid to examine the trends.
Planned upgrades of the Mark IIIfp include increasing the number of
processors to 128, and replacement of the I/O system will be
high-performance CIO (concurrent I/O) hardware. Further new Weitek
coprocessors, installed since the present calculations were done,
perform 64-bit floating-point arithmetic at about the same nominal peak
speed as the 32-bit boards. From the data in the present paper, it is
possible to predict with good reliability the performance of this
upgraded version of the Mark IIIfp (the CIO upgrade was never
performed). A CRAY Y-MP/864 was installed at the San Diego
Supercomputer Center and measurements show that it is about two times
faster than the CRAY X-MP/48 for the surface function code and 1.7
times faster for the logarithmic derivative code. In
Table 8.5, we summarize the available or predicted speed
information for the present codes for the current 64-processor and the
planned 128-processor Mark IIIfp, as well as the CRAY X-MP/48, CRAY 2,
and CRAY Y-MP/864 supercomputers. It can be seen that Mark IIIfp
machines are competitive with all of the currently available CRAYs
(operating as single-processor machines). The results described in
this paper demonstrate the feasibility of performing reactive
scattering calculations with high efficiency
in parallel fashion. As the number of processors continues to
increase, such parallel calculations in systems of greater complexity
will become practical in the not-too-distant future.
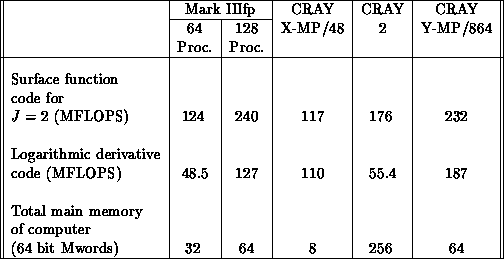
Table 8.5: Overall speed of reactive scattering codes on several machines.





Next: Studies of Electron-Molecule
Up: Quantum Mechanical Reactive
Previous: 8.2.3 Parallel Algorithm
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
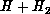 system on the LSTH
surface [Liu:73a], [Siegbahn:78a],
[Truhlar:78a;79a] for partial waves with total
angular momentum J = 0,1,2 and energies up to
system on the LSTH
surface [Liu:73a], [Siegbahn:78a],
[Truhlar:78a;79a] for partial waves with total
angular momentum J = 0,1,2 and energies up to 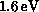 . Flux is
conserved to better than 1% for J = 0, 2.3% for J = 1, and 3.6%
for J = 2 for all open channels over the entire energy range considered.
. Flux is
conserved to better than 1% for J = 0, 2.3% for J = 1, and 3.6%
for J = 2 for all open channels over the entire energy range considered.






 (Upper Abscissa) for the
(Upper Abscissa) for the
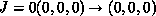
 Symmetry Transition in
Symmetry Transition in
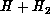 Collisions on the LSTH Potential Energy Surface. The symbol
Collisions on the LSTH Potential Energy Surface. The symbol
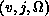 labels an asymptotic state of the
labels an asymptotic state of the 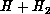 system in which
v, j, and
system in which
v, j, and 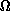 are the quantum numbers of the initial or final
are the quantum numbers of the initial or final 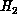 states. The vertical arrows on the upper abscissa denote the energies at
which the corresponding
states. The vertical arrows on the upper abscissa denote the energies at
which the corresponding 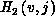 states open up. The length of those
arrows decreases as v spans the values 0, 1, and 2, and the numbers 0, 5,
and 10 associated with the arrows define a labelling for the value of j.
The number of LHSF used was 36 and the number of primitives used to calculate
these surface functions was 80.
states open up. The length of those
arrows decreases as v spans the values 0, 1, and 2, and the numbers 0, 5,
and 10 associated with the arrows define a labelling for the value of j.
The number of LHSF used was 36 and the number of primitives used to calculate
these surface functions was 80.
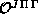 and interaction
and interaction 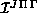 matrices) and the logarithmic derivative propagation code. For the surface
function code, the speeds on the first two machines are about the same.
The CRAY 2 is 1.43 times faster than the Mark IIIfp and 1.51 times faster
than the CRAY X-MP/48 for this code. The reason is that this program is
dominated by matrix-vector multiplications which are done in optimized
assembly code in all three machines. For this particular operation, the
CRAY 2 is 2.03 times faster than the CRAY X-MP/48 whereas, for more
memory-intensive operations, the CRAY 2 is slower than the CRAY X-MP/48
[
matrices) and the logarithmic derivative propagation code. For the surface
function code, the speeds on the first two machines are about the same.
The CRAY 2 is 1.43 times faster than the Mark IIIfp and 1.51 times faster
than the CRAY X-MP/48 for this code. The reason is that this program is
dominated by matrix-vector multiplications which are done in optimized
assembly code in all three machines. For this particular operation, the
CRAY 2 is 2.03 times faster than the CRAY X-MP/48 whereas, for more
memory-intensive operations, the CRAY 2 is slower than the CRAY X-MP/48
[
 ) of the parallel LHSF code was determined
using the definition
) of the parallel LHSF code was determined
using the definition 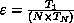 , where
, where
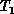 and
and 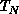 are, respectively, the implementation times using a
single-processor and N processors. The single processor times are
obtained from runs performed after removing the overhead of the
parallel code, that is, after removing the communication calls and some
logical statements. Perfect efficiency (
are, respectively, the implementation times using a
single-processor and N processors. The single processor times are
obtained from runs performed after removing the overhead of the
parallel code, that is, after removing the communication calls and some
logical statements. Perfect efficiency ( ) implies
that the N-processor hypercube is N times faster than a single
processor. In Figure
) implies
that the N-processor hypercube is N times faster than a single
processor. In Figure 
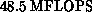 , which is about 44% of that of the CRAY X-MP/48
and 88% of that of the CRAY 2. As the number of channels increases,
the number of processors per cluster may be made larger in order to
increase the amount of memory available in each cluster. The
corresponding efficiency should continue to be adequate due to the
larger matrix dimensions involved.
, which is about 44% of that of the CRAY X-MP/48
and 88% of that of the CRAY 2. As the number of channels increases,
the number of processors per cluster may be made larger in order to
increase the amount of memory available in each cluster. The
corresponding efficiency should continue to be adequate due to the
larger matrix dimensions involved.

