




Next: 8.1.2 Basic Matrix Arithmetic
Up: 8.1 Full and Banded
Previous: 8.1 Full and Banded
The data decomposition (or distribution) is a major factor in determining the
efficiency of a concurrent matrix algorithm, so before
detailing the research into concurrent linear algebra done at Caltech, we
shall first introduce some basic decomposition strategies.
The processors of a concurrent computer can be uniquely labelled by
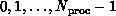 , where
, where 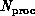 is the number of
processors. A vector of length M may be decomposed over the
processors by assigning the vector entry with global index m (where
is the number of
processors. A vector of length M may be decomposed over the
processors by assigning the vector entry with global index m (where
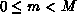 ) to processor p, where it is stored as the ientry
in a local array. Thus, the decomposition of a vector can be regarded
as a mapping of the global index, m, to an index pair,
) to processor p, where it is stored as the ientry
in a local array. Thus, the decomposition of a vector can be regarded
as a mapping of the global index, m, to an index pair, 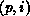 ,
specifying the processor number and local index.
,
specifying the processor number and local index.
For matrix problems, the processors are usually arranged as a 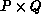 grid. Thus, the grid consists of P rows of processors and Q
columns of processors, and
grid. Thus, the grid consists of P rows of processors and Q
columns of processors, and 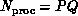 . Each processor can be uniquely
identified by its position,
. Each processor can be uniquely
identified by its position, 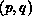 , on the processor grid. The
decomposition of an
, on the processor grid. The
decomposition of an 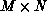 matrix can be regarded as the
Cartesian product of two vector decompositions,
matrix can be regarded as the
Cartesian product of two vector decompositions, 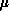 and
and  . The mapping
. The mapping 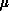 decomposes the M rows of the matrix
over the P processor rows, and
decomposes the M rows of the matrix
over the P processor rows, and  decomposes the N columns of
the matrix over the Q processor columns. Thus, if
decomposes the N columns of
the matrix over the Q processor columns. Thus, if 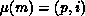 and
and
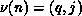 , then the matrix entry with global index
, then the matrix entry with global index 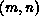 is
assigned to the processor at position
is
assigned to the processor at position 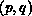 on the processor grid,
where it is stored in a local array with index
on the processor grid,
where it is stored in a local array with index 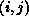 .
.
Two common decompositions are the linear and scattered
decompositions. The linear decomposition, 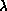 , assigns
contiguous entries in the global vector to the processors in blocks,
, assigns
contiguous entries in the global vector to the processors in blocks,
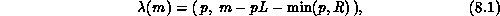
where
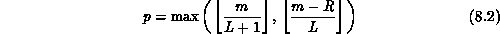
and 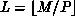 and
and 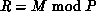 . The scattered decomposition,
. The scattered decomposition,
 , assigns consecutive entries in the global vector to different
processors,
, assigns consecutive entries in the global vector to different
processors,
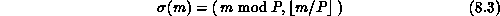
Figure 8.1 shows examples of these two types of decomposition
for a 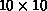 matrix.
matrix.

Figure 8.1: These Eight Figures Show Different Ways of Decomposing a
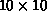 Matrix. Each cell represents a matrix entry, and is
labelled by the position,
Matrix. Each cell represents a matrix entry, and is
labelled by the position, 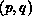 , in the processor grid of the
processor to which it is assigned. To emphasize the pattern of
decomposition, the matrix entries assigned to the processor in the
first row and column of the processor grid are shown shaded. Figures
(a) and (b) show linear and scattered row-oriented decompositions,
respectively, for four processors arranged as a
, in the processor grid of the
processor to which it is assigned. To emphasize the pattern of
decomposition, the matrix entries assigned to the processor in the
first row and column of the processor grid are shown shaded. Figures
(a) and (b) show linear and scattered row-oriented decompositions,
respectively, for four processors arranged as a 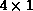 grid
(P=4, Q=1). In Figures (c) and (d), the corresponding
column-oriented decompositions are shown (P=1, Q=4). Figures (e)
through (h) show linear and scattered block-oriented decompositions for
16 processors arranged as a
grid
(P=4, Q=1). In Figures (c) and (d), the corresponding
column-oriented decompositions are shown (P=1, Q=4). Figures (e)
through (h) show linear and scattered block-oriented decompositions for
16 processors arranged as a 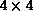 grid (P=Q=4).
grid (P=Q=4).
The mapping of processors onto the processor grid is determined by the
programming methodology, which in turn depends closely on the concurrent
hardware. For machines such as the nCUBE-1 hypercube, it
is advantageous to exploit any locality properties in the algorithm in
order to reduce communication costs. In such cases, processors may be
mapped onto the processor grid by a binary Gray code scheme
[Fox:88a], [Saad:88a], which ensures that adjacent processors
on the processor grid are directly connected by a communication
channel. For machines such as the Symult 2010, for which the time to
send a message between any two processors is almost independent of
their separation in the hardware topology, locality of communication is
not an issue, and the processors can be mapped arbitrarily onto the
processor grid.





Next: 8.1.2 Basic Matrix Arithmetic
Up: 8.1 Full and Banded
Previous: 8.1 Full and Banded
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
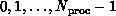 , where
, where 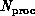 is the number of
processors. A vector of length M may be decomposed over the
processors by assigning the vector entry with global index m (where
is the number of
processors. A vector of length M may be decomposed over the
processors by assigning the vector entry with global index m (where
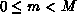 ) to processor p, where it is stored as the ientry
in a local array. Thus, the decomposition of a vector can be regarded
as a mapping of the global index, m, to an index pair,
) to processor p, where it is stored as the ientry
in a local array. Thus, the decomposition of a vector can be regarded
as a mapping of the global index, m, to an index pair, 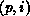 ,
specifying the processor number and local index.
,
specifying the processor number and local index.





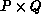 grid. Thus, the grid consists of P rows of processors and Q
columns of processors, and
grid. Thus, the grid consists of P rows of processors and Q
columns of processors, and 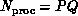 . Each processor can be uniquely
identified by its position,
. Each processor can be uniquely
identified by its position, 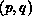 , on the processor grid. The
decomposition of an
, on the processor grid. The
decomposition of an 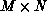 matrix can be regarded as the
Cartesian
matrix can be regarded as the
Cartesian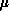 and
and  . The mapping
. The mapping 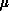 decomposes the M rows of the matrix
over the P processor rows, and
decomposes the M rows of the matrix
over the P processor rows, and  decomposes the N columns of
the matrix over the Q processor columns. Thus, if
decomposes the N columns of
the matrix over the Q processor columns. Thus, if 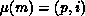 and
and
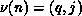 , then the matrix entry with global index
, then the matrix entry with global index 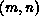 is
assigned to the processor at position
is
assigned to the processor at position 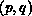 on the processor grid,
where it is stored in a local array with index
on the processor grid,
where it is stored in a local array with index 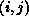 .
.
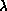 , assigns
contiguous entries in the global vector to the processors in blocks,
, assigns
contiguous entries in the global vector to the processors in blocks,
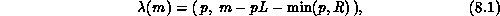
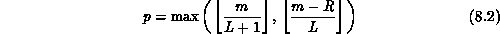
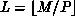 and
and 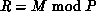 . The scattered decomposition,
. The scattered decomposition,
 , assigns consecutive entries in the global vector to different
processors,
, assigns consecutive entries in the global vector to different
processors,
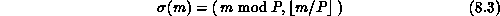
 matrix.
matrix.

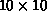 Matrix. Each cell represents a matrix entry, and is
labelled by the position,
Matrix. Each cell represents a matrix entry, and is
labelled by the position, 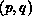 , in the processor grid of the
processor to which it is assigned. To emphasize the pattern of
decomposition, the matrix entries assigned to the processor in the
first row and column of the processor grid are shown shaded. Figures
(a) and (b) show linear and scattered row-oriented decompositions,
respectively, for four processors arranged as a
, in the processor grid of the
processor to which it is assigned. To emphasize the pattern of
decomposition, the matrix entries assigned to the processor in the
first row and column of the processor grid are shown shaded. Figures
(a) and (b) show linear and scattered row-oriented decompositions,
respectively, for four processors arranged as a 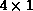 grid
(P=4, Q=1). In Figures (c) and (d), the corresponding
column-oriented decompositions are shown (P=1, Q=4). Figures (e)
through (h) show linear and scattered block-oriented decompositions for
16 processors arranged as a
grid
(P=4, Q=1). In Figures (c) and (d), the corresponding
column-oriented decompositions are shown (P=1, Q=4). Figures (e)
through (h) show linear and scattered block-oriented decompositions for
16 processors arranged as a 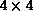 grid (P=Q=4).
grid (P=Q=4).