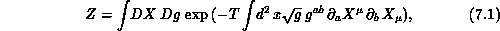





As a point particle in space moves through time, it traces out a line, called the worldline; similarly, as the string which looks like a line in space moves through time, it sweeps out a two-dimensional surface called the worldsheet. Thus, there are two ways in which to discretize the string:either the worldsheet is discretized or the (d-dimensional) space-time in which the string is embedded is discretized. We shall consider the former, which is referred to as the intrinsic approach; the latter is reviewed in [Ambjorn:89a]. Such discretized surface models fall into three categories:regular, fixed random, and dynamical random surfaces. In the first, the surface is composed of plaquettes in a d-dimensional regular hypercubic lattice; in the second, the surface is randomly triangulated once at the beginning of the simulation; and in the third, the random triangulation becomes dynamical (i.e., is changed during the simulation). It is these dynamically triangulated random surfaces we wish to simulate. Such a simulation is, in effect, that of a fluid surface. This is because the varying triangulation means that there is no fixed reference frame, which is precisely what one would expect of a fluid where the molecules at two different points could interchange and still leave the surface intact. In string theory, this is called reparametrization invariance. If, instead, one used a regular surface, one would be simulating a tethered or crystalline surface on which there is considerable literature (see [Ambjorn:89b] for a survey of the work in the field). In this case, the molecules of the surface are frozen in a fixed array. There have also been simulations of fixed random surfaces; see, for example, [Baig:89a]. One other reason for studying random surface models is to understand integration over geometrical objects and discover whether the nonperturbative discretization procedures, which work so well for local field theories like QCD, can be applied successfully.
The partition function describing the quantum mechanics of a surface was first formulated by Polyakov [Polyakov:81a]. For a bosonic string embedded in d-dimensions, it is written as
where 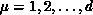 labels the dimensions of the embedding space,
a,b = 1,2 are the coordinates on the worldsheet, and T is the string
tension. The integration is over both the fields
labels the dimensions of the embedding space,
a,b = 1,2 are the coordinates on the worldsheet, and T is the string
tension. The integration is over both the fields 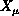 and the metric on
the worldsheet
and the metric on
the worldsheet  .
. 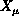 gives the embedding of the
two-dimensional worldsheet swept out by the string in the d-dimensional
space in which it lives. If we integrate over the metric, we obtain an area
action for the worldsheet,
gives the embedding of the
two-dimensional worldsheet swept out by the string in the d-dimensional
space in which it lives. If we integrate over the metric, we obtain an area
action for the worldsheet,
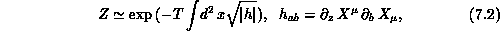
which is a direct generalization of the length action for a particle, i.e.,
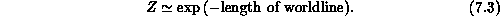
We can thus see that the action in Equation 7.1 is the natural area action that one might expect for a surface whose dynamics were determined by the surface tension.
The first discretized model of this partition function was suggested independently by three groups:[Ambjorn:85a], [David:85a], and [Kazakov:85a].

where the outer sum runs over some set T of allowed triangulations of the
surface, weighted by their importance factors  , and is supposed to
represent the effect of the metric integration in the path integral. The
inner sum in the exponential is over the edges
, and is supposed to
represent the effect of the metric integration in the path integral. The
inner sum in the exponential is over the edges  of the
triangulation, or mesh, and working with a fixed number of nodes N
corresponds to working in a microcanonical ensemble of fixed intrinsic area.
The model is that of a dynamically triangulated surface because one is
instructed to perform the sum over different triangulations, so both
the fields,
of the
triangulation, or mesh, and working with a fixed number of nodes N
corresponds to working in a microcanonical ensemble of fixed intrinsic area.
The model is that of a dynamically triangulated surface because one is
instructed to perform the sum over different triangulations, so both
the fields, 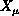 on the mesh and the mesh itself, are dynamical objects.
on the mesh and the mesh itself, are dynamical objects.
A considerable amount of effort has been devoted to simulating this pure area action, both in microcanonical form with a fixed number of nodes [Billoire:86a], [Boulatov:86a], [Jurkiewicz:86a] and in grand canonical form, where the number of nodes is allowed to change in a manner which satisfies detailed balance [Ambjorn:87b], [David:87a], [Jurkiewicz:86b]. (This allows measurements to be made of how the partition function varies with the number of nodes N, which determines an exponent called the string susceptibility.) The results are rather disappointing, in that the surfaces appear to be in a very crumpled state, as can be seen from measuring the gyration radius X2, which gives a figure for the ``mean size'' of the surface. Its discretized form is
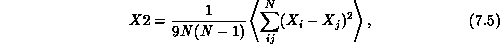
where the sum now runs over all pairs of
nodes ij. X2 is observed to grow only logarithmically with N.
This means that the Hausdorff dimension,
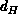 , which measures how the surface grows upon the addition of
intrinsic area and is defined by
, which measures how the surface grows upon the addition of
intrinsic area and is defined by
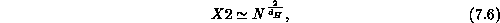
is infinite. Analytical work [Durhuus:84a] shows that the string tension fails to scale in the continuum limit so that, heuristically speaking, it becomes so strong that it collapses the surface into something like a branched polymer. Thus, the pure area action does not provide a good continuum limit. It was observed in [Ambjorn:85a] and [Espriu:87a] that another way to understand the pathological behavior of the simulations, was to note that spikelike configurations in the surface were not suppressed by the area action, allowing it to degenerate into a spiky, crumpled object. An example of such a configuration is shown in Figure 7.2(a).
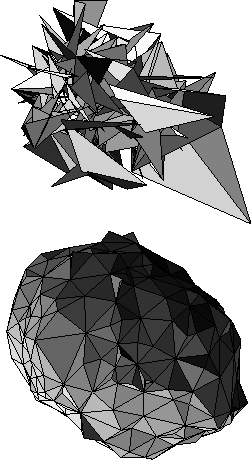
Figure 7.2: (a) Crumpled Phase (b) Smooth Phase
To overcome this difficulty, one uses the fact that adding to the pure area action a term in the extrinsic curvature squared (as originally suggested by Polyakov [Polyakov:86a] and Kleinert [Kleinert:86a] for string models of hadron interactions) smooths out the surface. In three dimensions, the extrinsic curvature of a two-dimensional surface is given by

where the rs are the principle radii of curvature at a point x on the surface. Two discretized forms of this extrinsic curvature term are possible, namely
where the inner sum is over the neighbors j of a node i and  is
the sum of the areas of the surrounding triangles as shown in
Figure 7.3; and
is
the sum of the areas of the surrounding triangles as shown in
Figure 7.3; and
where one takes the dot product of the unit normals  of
triangles which share a common edge
of
triangles which share a common edge  . For
sufficiently large values of the
. For
sufficiently large values of the  coupling, the worldsheet is
smooth, as shown in Figure 7.2(b). Analytical work
[Ambjorn:87a;89b] strongly
suggests, however, that a continuum limit will only be found in the
limit of infinite extrinsic curvature coupling.
coupling, the worldsheet is
smooth, as shown in Figure 7.2(b). Analytical work
[Ambjorn:87a;89b] strongly
suggests, however, that a continuum limit will only be found in the
limit of infinite extrinsic curvature coupling.
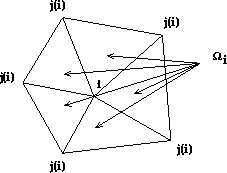
Figure: Illustration of First Form of Extrinsic Curvature
(Equation 7.8)
It came as something of a surprise, therefore, when a simulation by
Catterall [Catterall:89a] revealed that the discretization
(Equation 7.8) seems to give a third-order phase
transition to the smooth phase and the discretization
(Equation 7.9) a second-order phase
transition, the latter offering the possibility
of defining a continuum limit at a finite value of the
extrinsic curvature coupling (because of the divergence of correlation
length at a second-order transition). Further work by Baillie,
Johnston, and Williams [Baillie:90j] confirmed the existence of
this ``crumpling transition.'' Typical
results, for a surface consisting of 288 nodes, are shown in the series
of Figure 7.4 (Color Plate), for the discretization of
Equation 7.8. The extrinsic curvature coupling,
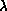 , is increased from 0 (the crumpled phase) to
, is increased from 0 (the crumpled phase) to  (the
smooth phase). We estimate that the crumpling transition is around
(the
smooth phase). We estimate that the crumpling transition is around
 .
.
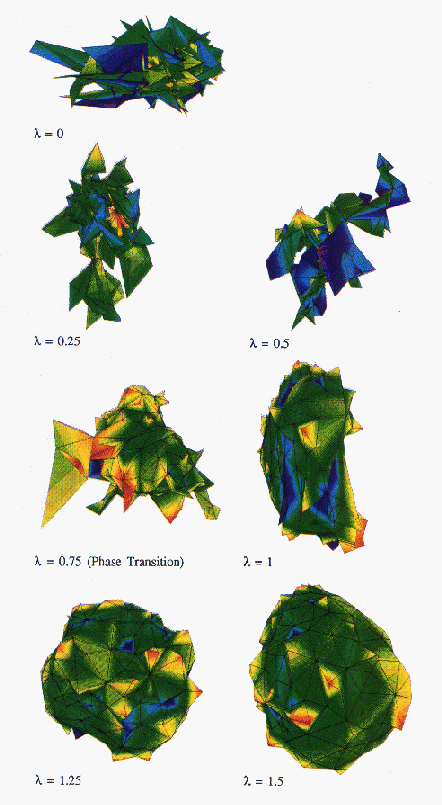
Figure 7.4: A 288-node DTRS uncrumpling as 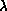 changes from 0 to 1.5.
changes from 0 to 1.5.
Further studies of the crumpling transition using the ``edge action'' discretization (Equation 7.9) have recently been performed [Ambjorn:92a], [Bowick:93a] on larger lattices in order to see whether this is a genuine phase transition, or just a finite size effect due to the small mesh sizes which had been simulated.
To summarize, a dynamically triangulated random surface with a pure area action does not offer a good discretization of a bosonic string or of a fluid surface. The addition of an extrinsic curvature term appears to give a crumpling transition between a smooth and crumpled phase, but the nature of this transition is unclear. In order for the continuum limit to give a string theory, it is necessary that there be a second-order phase transition, so that the correlation length diverges and the details of the lattice discretization are irrelevant, as in lattice QCD (see Section 4.3).




