




Next: Nonsymmetric Eigenproblems
Up: Computational Routines
Previous: Generalized RQ factorization
Let A be a real symmetric or
complex Hermitian n-by-n matrix.
A scalar 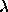 is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if
is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if 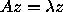 .
. 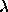 is
always real when A is real symmetric or complex Hermitian.
is
always real when A is real symmetric or complex Hermitian.
The basic task of the symmetric eigenproblem routines is to compute values of 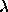 and, optionally, corresponding vectors z for a given matrix A.
and, optionally, corresponding vectors z for a given matrix A.
This computation proceeds in the following stages:
- The real symmetric or complex Hermitian matrix A is reduced to
real tridiagonal form
T.
If A is real symmetric, the decomposition is
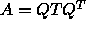 with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is
with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is 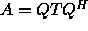 with Q unitary and T, as before,
real symmetric tridiagonal .
with Q unitary and T, as before,
real symmetric tridiagonal .
- Eigenvalues and eigenvectors of the real symmetric tridiagonal matrix
T are computed.
If all eigenvalues and eigenvectors are computed, this process is equivalent to
factorizing T as
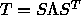 , where S is orthogonal and
, where S is orthogonal and 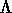 is diagonal.
The diagonal entries of
is diagonal.
The diagonal entries of 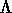 are the eigenvalues of T, which are also
the eigenvalues of A, and the
columns of S are the eigenvectors of T; the eigenvectors of A are
the columns of Z=QS, so that
are the eigenvalues of T, which are also
the eigenvalues of A, and the
columns of S are the eigenvectors of T; the eigenvectors of A are
the columns of Z=QS, so that 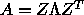 (
(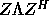 when
A is complex Hermitian).
when
A is complex Hermitian).
In the real case, the decomposition 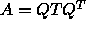 is computed by
the routine PxSYTRD
(see table 3.8). The complex analogue of this routine
is called PxHETRD.
The routine PxSYTRD (or PxHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section 3.4.
The routine PxORMTR (or in the complex case PxUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T, computed by PxSTEIN, back to eigenvectors of A.
is computed by
the routine PxSYTRD
(see table 3.8). The complex analogue of this routine
is called PxHETRD.
The routine PxSYTRD (or PxHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section 3.4.
The routine PxORMTR (or in the complex case PxUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T, computed by PxSTEIN, back to eigenvectors of A.
The following routines compute eigenvalues and eigenvectors of T.
- xSTEQR2
-
This routine [77] is a modified version of LAPACK routine xSTEQR.
It has fewer iterations than the LAPACK routine due to a modification
in the look-ahead technique described in [77].
Some additional modifications allow each process to perform partial updates
to matrix Q.
This routine computes all eigenvalues and, optionally, eigenvectors of a
symmetric tridiagonal matrix using the implicit QL or QR method.
- PxSTEBZ
- This routine uses bisection to compute some or all of the
eigenvalues. Options provide for computing all the eigenvalues in a real
interval or all the eigenvalues
from the ith to the jth largest.
It can be highly accurate but may be adjusted to run faster if lower
accuracy is acceptable.
- PxSTEIN
-
Given accurate eigenvalues, this routine uses inverse
iteration to compute some or all of the eigenvectors.
Without any reorthogonalization, inverse iteration may produce vectors
that have large dot products. To cure this, most implementations of
inverse iteration such as LAPACK's
xSTEIN reorthogonalize when eigenvalues differ
by less than 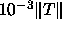 . As a result, the eigenvectors computed
by xSTEIN are almost always orthogonal, but the increase in cost can result
in
. As a result, the eigenvectors computed
by xSTEIN are almost always orthogonal, but the increase in cost can result
in 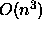 work. On some rare examples, xSTEIN may still fail to deliver
accurate answers; see [43, 44]. The orthogonalization
done by PxSTEIN is limited by the amount of workspace provided; whenever
it performs less reorthogonalization than xSTEIN, there is a danger that the
dot products may not be satisfactory.
work. On some rare examples, xSTEIN may still fail to deliver
accurate answers; see [43, 44]. The orthogonalization
done by PxSTEIN is limited by the amount of workspace provided; whenever
it performs less reorthogonalization than xSTEIN, there is a danger that the
dot products may not be satisfactory.
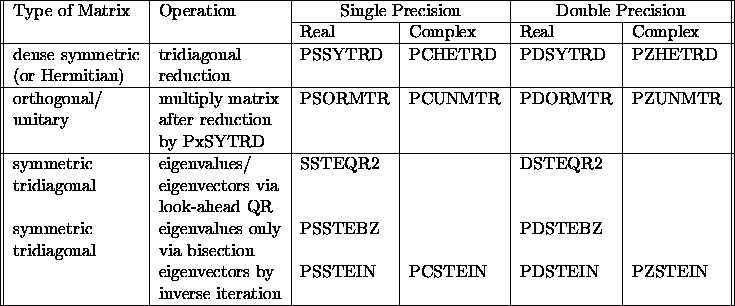
Table 3.8: Computational routines for the symmetric eigenproblem





Next: Nonsymmetric Eigenproblems
Up: Computational Routines
Previous: Generalized RQ factorization
Susan Blackford
Tue May 13 09:21:01 EDT 1997
![]() is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if
is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if ![]() .
. ![]() is
always real when A is real symmetric or complex Hermitian.
is
always real when A is real symmetric or complex Hermitian.
![]() and, optionally, corresponding vectors z for a given matrix A.
and, optionally, corresponding vectors z for a given matrix A.
![]() is computed by
the routine PxSYTRD
(see table 3.8). The complex analogue of this routine
is called PxHETRD.
The routine PxSYTRD (or PxHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section 3.4.
The routine PxORMTR (or in the complex case PxUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T, computed by PxSTEIN, back to eigenvectors of A.
is computed by
the routine PxSYTRD
(see table 3.8). The complex analogue of this routine
is called PxHETRD.
The routine PxSYTRD (or PxHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section 3.4.
The routine PxORMTR (or in the complex case PxUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T, computed by PxSTEIN, back to eigenvectors of A.
![]() . As a result, the eigenvectors computed
by xSTEIN are almost always orthogonal, but the increase in cost can result
in
. As a result, the eigenvectors computed
by xSTEIN are almost always orthogonal, but the increase in cost can result
in ![]() work. On some rare examples, xSTEIN may still fail to deliver
accurate answers; see [43, 44]. The orthogonalization
done by PxSTEIN is limited by the amount of workspace provided; whenever
it performs less reorthogonalization than xSTEIN, there is a danger that the
dot products may not be satisfactory.
work. On some rare examples, xSTEIN may still fail to deliver
accurate answers; see [43, 44]. The orthogonalization
done by PxSTEIN is limited by the amount of workspace provided; whenever
it performs less reorthogonalization than xSTEIN, there is a danger that the
dot products may not be satisfactory.
