Simplifying Assumptions Used in Example Program

Several simplifying assumptions and/or restrictions have been made in this example program in order to present the most basic example for the user:

• We have chosen a small block size, MB=NB=2; however, this should not be regarded as a typical choice of block size in a user's application. For best performance, a choice of MB=NB=32 or MB=NB=64 is more suitable. Refer to Chapter 5 for further details.
• A simplistic subroutine MATINIT is used to assign matrices A and B to the process grid. Note that this subroutine hardcodes the local arrays on each process and does not perform communication. It is not a ScaLAPACK routine and is provided only for the purposes of this example program.
• We assume RSRC=CSRC=0 , and thus both matrices A and B are distributed across the process grid starting with process (0,0). In general, however, any process in the current process grid can be assigned to receive the first element of the distributed matrix.
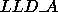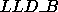• We have set the local leading dimension of local array A and the local leading dimension of local array B to be the same over all process rows in the process grid. The variable MXLLDA is equal to the maximum local leading dimension for array A (denoted ) over all process rows. Likewise, variable MXLLDB is the maximum local leading dimension for array B (denoted ) over all process rows. In general, however, the local leading dimension of the local array can differ from process to process in the process grid.
• The system is solved by using the entire matrix A, as opposed to a submatrix of A, so the global indices, denoted by IA, JA, IB, and JB     , into the matrix are equal to 1. Refer to figure 4.7 in section 4.3.5 for more information on the representation of global addressing into a distributed submatrix.