Error Bounds for Linear Least Squares Problems

 

The linear least squares problem is to find x that minimizes . We discuss error bounds for the most common case where A is m-by-n with m > n, and A has full rank ; this is called an overdetermined least squares problem   (the following code fragments deal with m=n as well).

Let be the solution computed by the driver routine PxGELS (see section 3.2.2). An approximate error bound     

may be computed in the following way:

      EPSMCH = PSLAMCH( ICTXT, 'E' )
*     Get the 2-norm of the right hand side B
      BNORM = PSLANGE( 'F', M, 1, B, IB, JB, DESCB, WORK )
*     Solve the least squares problem; the solution X overwrites B
      CALL PSGELS( 'N', M, N, 1, A, IA, JA, DESCA, B, IB, JB, DESCB,
     $             WORK, LWORK, INFO )
      IF( MIN( M, N ).GT.0 ) THEN
*        Get the 2-norm of the residual A*X-B
         RNORM = PSLANGE( 'F', M-N, 1, B, IB+N, JB, DESCB, WORK ) 
*        Get the reciprocal condition number RCOND of A
         CALL PSTRCON( 'I', 'U', 'N', N, A, IA, JA, DESCA, RCOND, WORK,
     $                 LWORK, IWORK, LIWORK, INFO )
         RCOND = MAX( RCOND, EPSMCH )
         IF( BNORM.GT.0.0 ) THEN
            SINT = RNORM / BNORM
         ELSE
            SINT = 0.0
         END IF
         COST = MAX( SQRT( ( 1.0E0 - SINT )*( 1.0E0 + SINT ) ), EPSMCH )
         TANT = SINT / COST
         ERRBD = EPSMCH*( 2.0E0 / ( RCOND*COST ) + TANT / RCOND**2 )
      END IF

 

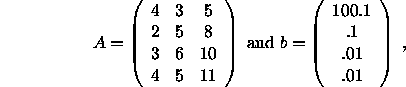
For example, if ,

then, to four decimal places,

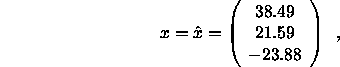
, , , , and the true error is .

Note that in the preceding code fragment, the routine PSLANGE was used to compute the two-norm of the right hand side matrix B and the residual . This routine was chosen because the result of the computation (BNORM or RNORM, respectively) is automatically known on all process columns within the process grid. The routine PSNRM2 could have also been used to perform this calculation; however, the use of PSNRM2 in this example would have required an additional communication broadcast, because the resulting value of BNORM or RNORM, respectively, is known only within the process column owning B(:,JB).

Further Details: Error Bounds for Linear Least Squares Problems 

The conventional error analysis of linear least squares problems goes as follows . As above, let be the solution to minimizing computed by ScaLAPACK using the least squares driver PxGELS (see section 3.2.2). We discuss the most common case, where A is overdetermined  (i.e., has more rows than columns) and has full rank [71]:     

The computed solution has a small normwise backward error. In other words, minimizes , where E and f satisfy    

and p(n) is a modestly growing function of n. We take p(n)=1 in the code fragments above. Let (approximated by 1/RCOND in the above code fragments), (= RNORM above), and (SINT = RNORM / BNORM above). Here, is the acute angle between the vectors and b.     Then when is small, the error is bounded by

where = COST and = TANT in the code fragments above.

We avoid overflow by making sure RCOND and COST are both at least EPSMCH, and by handling the case of a zero B matrix separately (BNORM = 0).    

may be computed directly from the singular values of A returned by PxGESVD. It may also be approximated by using PxTRCON following calls to PxGELS. PxTRCON estimates or instead of , but these can differ from by at most a factor of n.