An important performance metric is parallel efficiency. Parallel
efficiency, E(N, P),
for a problem of size N on P nodes is
defined in the usual
way [65, 92] by
where T(N,P) is the
runtime of the parallel algorithm, and 
is the runtime
of the best sequential
algorithm. For dense
matrix computations,
an implementation is
said to be scalable
if the parallel efficiency
is an increasing function
of 
, the problem
size per node. The
algorithms implemented in
the ScaLAPACK library are
scalable in this sense.
Figure 5.1 shows the scalability of the ScaLAPACK implementation of the LU factorization on the Intel XP/S Paragon computer. The nodes of the Intel XP/S Paragon computer are general-purpose (GP) or multiprocessor (MP) nodes, based on the Intel i860 XP RISC processors. Each Intel i860 processor is capable of a peak performance of 50 Mflop/s. On such a processor, however, the vendor-supplied BLAS matrix-matrix multiply routine DGEMM can achieve only approximately 45 Mflop/s. The computer used for obtaining the performance results presented in this chapter consisted of MP nodes configured as follows: each MP node had three Intel i860 XP processors -- two to execute application code and a third used exclusively as a message coprocessor . On such a node, the vendor-supplied BLAS matrix-matrix multiply routine DGEMM can achieve approximately 90 Mflop/s.
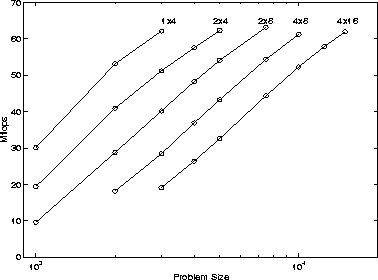
Figure 5.1: LU Performance per Intel XP/S MP Paragon node
Figure 5.1 shows the speed in Mflop/s per node of the ScaLAPACK LU factorization routine PDGETRF for different computer configurations. This figure illustrates that when the number of nodes is scaled by a constant factor, the same efficiency or speed per node is achieved for equidistant problem sizes on a logarithmic scale. In other words, maintaining a constant memory use per node allows efficiency to be maintained. (This scalability behavior is also referred to as isoefficiency, or isogranularity .) In practice, however, a slight degradation is acceptable. The ScaLAPACK driver routines, in general, feature the same scalability behavior up to a constant factor that depends on the exact number of floating-point operations and the total volume of data exchanged during the computation.
In large dense linear
algebra computations,
the computation
cost dominates the
communication cost.
In the following, the
time to execute one
floating-point operation
by one node is denoted
by 
. The time to
communicate a message
between two nodes is
approximated by a
linear function of
the number of items
communicated. The function
is the sum of the time
to prepare the message
for transmission (
)
and the time taken
by the message
to traverse the
network to its
destination, that is,
the product of its
length by the time
to transfer one
data item (
) .
Alternatively,
is also called the
latency, since
it is the time to
communicate a
message of zero
length. On most
modern interconnection
networks, the order of
magnitude of the latency
varies between a
microsecond and a
millisecond.
The bandwidth of
the network is also referred to as
its throughput.
It is proportional to the reciprocal of . On modern
networks, the order of magnitude of the bandwidth is the
megabyte per second. For a scalable algorithm with
held constant, one expects the performance to
be proportional to P. The algorithms implemented in
ScaLAPACK are scalable in this sense. Table 5.1
summarizes the relevant constants used in our scalability
analysis.
Table 5.1: Variable definitions
Using the notation presented in table 5.1,
the execution time of the ScaLAPACK drivers can be
approximated by
The corresponding parallel efficiency
can then be approximated by
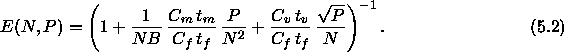
Equation 5.2 illustrates, in particular, that
the communication versus computation performance ratio of a
distributed-memory computer significantly affects parallel efficiency. The
ratio of the latency to the time per flop 
greatly
affects the parallel efficiency of small problems. The ratio
of the network throughput to the flop rate 
significantly affects the parallel efficiency of medium-sized
problems. For large problems, the node flop rate 
is the dominant factor contributing to the parallel
efficiency of the parallel algorithms implemented in ScaLAPACK.