As mentioned earlier, tree computations
typically exhibit a tree-like
process control structure which also conforms to the communication pattern
in many instances. To illustrate this model, we consider a parallel sorting
algorithm that works as follows. One process (the manually started
process in PVM) possesses (inputs or generates) the list to be sorted.
It then spawns a second process and sends it half the list. At this
point, there are two processes each of which spawns a process and sends
them one-half of their already halved lists. This continues until
a tree of appropriate depth is constructed. Each process then independently
sorts its portion of the list, and a merge phase follows where sorted
sublists are transmitted upwards along the tree edges, with intermediate
merges being done at each node. This algorithm is illustrative of
a tree computation in which the workload is known in advance; a diagram
depicting the process is given in Figure ![]() ;
an algorithmic outline is given below.
;
an algorithmic outline is given below.
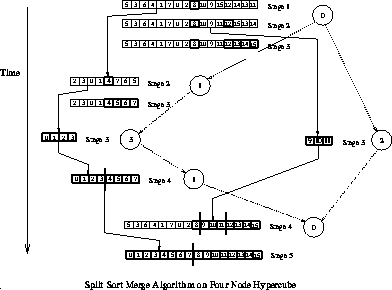
Figure: Tree-computation example
{ Spawn and partition list based on a broadcast tree pattern. }
for i := 1 to N, such that 2^N = NumProcs
forall processors P such that P < 2^i
pvm_spawn(...) {process id P XOR 2^i}
if P < 2^(i-1) then
midpt: = PartitionList(list);
{Send list[0..midpt] to P XOR 2^i}
pvm_send((P XOR 2^i),999)
list := list[midpt+1..MAXSIZE]
else
pvm_recv(999) {receive the list}
endif
endfor
endfor
{ Sort remaining list. }
Quicksort(list[midpt+1..MAXSIZE])
{ Gather/merge sorted sub-lists. }
for i := N downto 1, such that 2^N = NumProcs
forall processors P such that P < 2^i
if P > 2^(i-1) then
pvm_send((P XOR 2^i),888)
{Send list to P XOR 2^i}
else
pvm_recv(888) {receive temp list}
merge templist into list
endif
endfor
endfor