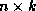 matrix
matrix 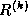 by
by
As discussed by Paige and Saunders in [168] and by Golub and Van Loan in [109], it is straightforward to derive the conjugate gradient method for solving symmetric positive definite linear systems from the Lanczos algorithm for solving symmetric eigensystems and vice versa. As an example, let us consider how one can derive the Lanczos process for symmetric eigensystems from the (unpreconditioned) conjugate gradient method.
Suppose we define the 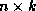 matrix
matrix 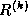 by
by
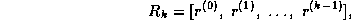
and the  upper bidiagonal matrix
upper bidiagonal matrix  by
by
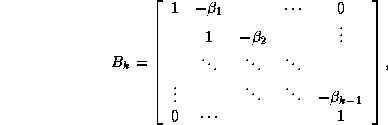
where the sequences  and
and 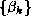 are defined by the standard
conjugate gradient algorithm discussed in §
are defined by the standard
conjugate gradient algorithm discussed in §![]() .
From the equations
.
From the equations
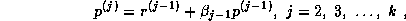
and  , we have
, we have 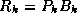 , where
, where
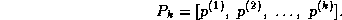
Assuming the elements of the sequence  are
are  -conjugate,
it follows that
-conjugate,
it follows that

is a tridiagonal matrix since

Since span{ } =
span{
} =
span{ } and since the elements of
} and since the elements of
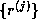 are mutually orthogonal, it can be shown that the columns of
are mutually orthogonal, it can be shown that the columns of
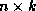 matrix
matrix  form an orthonormal basis
for the subspace
form an orthonormal basis
for the subspace 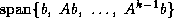 , where
, where
 is a diagonal matrix whose
is a diagonal matrix whose 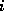 th diagonal element is
th diagonal element is 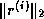 . The columns of the matrix
. The columns of the matrix 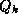 are the Lanczos vectors (see
Parlett [171]) whose associated projection of
are the Lanczos vectors (see
Parlett [171]) whose associated projection of  is
the tridiagonal matrix
is
the tridiagonal matrix
The extremal eigenvalues of 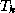 approximate those of the
matrix
approximate those of the
matrix  . Hence,
the diagonal and subdiagonal elements of
. Hence,
the diagonal and subdiagonal elements of 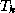 in
(
in
(![]() ), which are readily available during iterations of the
conjugate gradient algorithm (§
), which are readily available during iterations of the
conjugate gradient algorithm (§![]() ),
can be used to construct
),
can be used to construct 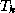 after
after  CG iterations. This
allows us to obtain good approximations to the extremal eigenvalues
(and hence the condition number) of the matrix
CG iterations. This
allows us to obtain good approximations to the extremal eigenvalues
(and hence the condition number) of the matrix  while we are generating
approximations,
while we are generating
approximations, 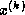 , to the solution of the linear system
, to the solution of the linear system  .
.
For a nonsymmetric matrix  , an equivalent nonsymmetric Lanczos
algorithm (see Lanczos [142]) would produce a
nonsymmetric matrix
, an equivalent nonsymmetric Lanczos
algorithm (see Lanczos [142]) would produce a
nonsymmetric matrix 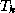 in (
in (![]() ) whose extremal eigenvalues
(which may include complex-conjugate pairs) approximate those of
) whose extremal eigenvalues
(which may include complex-conjugate pairs) approximate those of  .
The nonsymmetric Lanczos method is equivalent to the BiCG method
discussed in §
.
The nonsymmetric Lanczos method is equivalent to the BiCG method
discussed in §![]() .
.