 are updated in each iteration by a multiple
are updated in each iteration by a multiple
 of the
search direction vector
of the
search direction vector  :
:
The Conjugate Gradient method is an effective method for symmetric positive definite systems. It is the oldest and best known of the nonstationary methods discussed here. The method proceeds by generating vector sequences of iterates (i.e., successive approximations to the solution), residuals corresponding to the iterates, and search directions used in updating the iterates and residuals. Although the length of these sequences can become large, only a small number of vectors needs to be kept in memory. In every iteration of the method, two inner products are performed in order to compute update scalars that are defined to make the sequences satisfy certain orthogonality conditions. On a symmetric positive definite linear system these conditions imply that the distance to the true solution is minimized in some norm.
The iterates  are updated in each iteration by a multiple
are updated in each iteration by a multiple
 of the
search direction vector
of the
search direction vector  :
:

Correspondingly the residuals  are updated as
are updated as
The choice 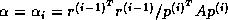 minimizes
minimizes 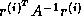 over all possible choices for
over all possible choices for  in
equation (
in
equation (![]() ).
).
The search directions are updated using the residuals
where the choice  ensures
that
ensures
that  and
and 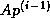 - or equivalently,
- or equivalently,
 and
and 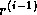 - are orthogonal . In fact, one can
show that this choice of
- are orthogonal . In fact, one can
show that this choice of  makes
makes  and
and  orthogonal to
all previous
orthogonal to
all previous 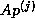 and
and  respectively.
respectively.
The pseudocode for the Preconditioned Conjugate Gradient Method is
given in Figure ![]() . It uses a preconditioner
. It uses a preconditioner  ;
for
;
for  one obtains the unpreconditioned version of the Conjugate Gradient
Algorithm. In that case the algorithm may be further simplified by skipping
the ``solve'' line, and replacing
one obtains the unpreconditioned version of the Conjugate Gradient
Algorithm. In that case the algorithm may be further simplified by skipping
the ``solve'' line, and replacing  by
by 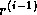 (and
(and 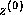 by
by 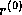 ).
).

Figure: The Preconditioned Conjugate Gradient Method