




Next: Examples
Up: General Linear Systems
Previous: Purpose
Contents
Index
- AB
- (input/output) REAL or COMPLEX
rectangular array, shape
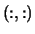 with
with
 and
and
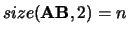 , where
, where
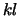 and
and 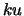 are, respectively, the numbers of subdiagonals and
superdiagonals in the band of
are, respectively, the numbers of subdiagonals and
superdiagonals in the band of  , and
, and 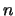 is the order of
is the order of  .
.
On entry, the matrix  in band storage. The
in band storage. The 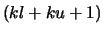 diagonals of
diagonals of  are stored in rows
are stored in rows  to
to 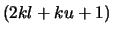 of AB,
so that the
of AB,
so that the 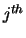 column of
column of  is stored in the
is stored in the 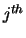 column of AB as follows:
column of AB as follows:
The remaining elements in 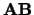 need not be set.
need not be set.
On exit, details of the factorization. 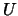 is an upper
triangular band matrix with
is an upper
triangular band matrix with 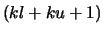 diagonals. These are stored
in the first
diagonals. These are stored
in the first 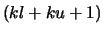 rows of
rows of 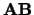 . The multipliers
that arise during the factorization are stored in the remaining rows.
. The multipliers
that arise during the factorization are stored in the remaining rows.
- B
- (input/output) REAL or COMPLEX array, shape
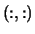 with
with
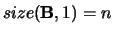 or shape
or shape 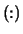 with
with
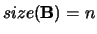 .
.
On entry, the matrix 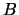 .
.
On exit, the solution matrix 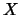 .
.
- KL
- Optional (input) INTEGER.
The number of subdiagonals in the band of  (
(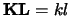 ).
).
The number of superdiagonals in the band is given by
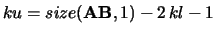 .
.
Default value:
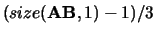 .
.
- IPIV
- Optional (output) INTEGER array,
shape
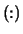 with
with
 .
.
The pivot indices that define the row interchanges; row 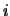 of
the matrix was interchanged with row
of
the matrix was interchanged with row
 .
.
- INFO
- Optional (output) INTEGER
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if INFO $= ...
...he factor $U$ is singular, so the solution could not be computed.
\end{infoarg}](img296.gif)
If 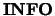 is not present and an error occurs, then the program
is terminated with an error message.
is not present and an error occurs, then the program
is terminated with an error message.
References: [1] and [17,9,20].





Next: Examples
Up: General Linear Systems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
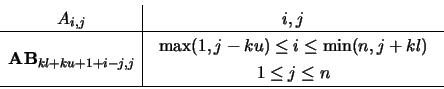
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if INFO $= ...
...he factor $U$ is singular, so the solution could not be computed.
\end{infoarg}](img296.gif)