




Next: Examples
Up: Standard Symmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
- AB
- (input/output) REAL or COMPLEX array,
shape
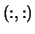 with
with 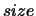 (AB,1)
(AB,1) 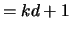 and
and 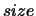 (AB,2)
(AB,2) 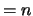 ,
where
,
where 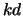 is the number of subdiagonals or superdiagonals in the
band and
is the number of subdiagonals or superdiagonals in the
band and 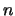 is the order of
is the order of  .
.
On entry, the upper (if UPLO = 'U') or lower
(if UPLO = 'L') triangle of matrix  in band storage.
The
in band storage.
The 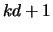 diagonals of
diagonals of  are stored in the rows of AB so
that the
are stored in the rows of AB so
that the 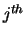 column of
column of  is
stored in the
is
stored in the 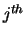 column of
column of 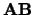 as follows:
as follows:
On exit, 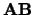 is overwritten by values generated during
the reduction of
is overwritten by values generated during
the reduction of  to a tridiagonal matrix
to a tridiagonal matrix 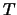 .
If
.
If 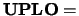 'U', the first superdiagonal and the diagonal
of
'U', the first superdiagonal and the diagonal
of 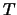 are returned in rows
are returned in rows 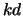 and
and 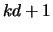 of
of 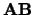 .
If
.
If 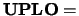 'L', the diagonal and first subdiagonal of
'L', the diagonal and first subdiagonal of
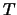 are returned in the first two rows of
are returned in the first two rows of 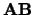 .
.
- W
- (output) REAL array, shape
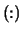 with
with
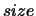 (W)
(W) 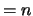 .
.
The eigenvalues in ascending order.
- UPLO
- Optional (input) CHARACTER(LEN=1).
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
Default value: 'U'.
- Z
- Optional (output) REAL or COMPLEX
square array, shape
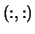 with
with 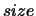 (Z,1)
(Z,1) 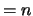 .
.
The columns of Z contain the orthonormal eigenvectors of  in the order of the eigenvalues.
in the order of the eigenvalues.
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO}...
...nts of an intermediate tridiagonal
form did not converge to zero.
\end{infoarg}](img608.gif)
If 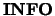 is not present and an error occurs, then the
program is terminated with an error message.
is not present and an error occurs, then the
program is terminated with an error message.
References: [1] and [17,9,20].





Next: Examples
Up: Standard Symmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
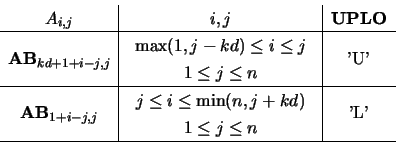
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO}...
...nts of an intermediate tridiagonal
form did not converge to zero.
\end{infoarg}](img608.gif)
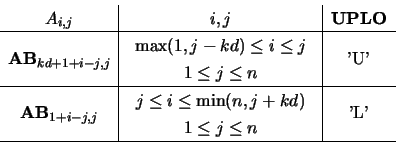
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO}...
...nts of an intermediate tridiagonal
form did not converge to zero.
\end{infoarg}](img608.gif)