




Next: Example (from Program LA_GELSY_EXAMPLE)
Up: Linear Least Squares Problems
Previous: Purpose
Contents
Index
- A
- (input/output) REAL or COMPLEX
array, shape
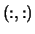 .
.
On entry, the matrix  .
.
On exit,  has been overwritten by details of its
complete orthogonal factorization.
has been overwritten by details of its
complete orthogonal factorization.
- B
- (input/output) REAL or COMPLEX array,
shape
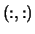 with
with 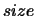 (B,1)
(B,1) 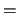
 (A,1),
(A,1),
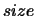 (A,2)) or shape
(A,2)) or shape  with
with  =
=
 (A,1),
(A,1), 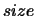 (A,2)).
(A,2)).
On entry, the matrix 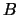 .
.
On exit, rows 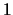 to
to 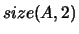 contain the solution matrix
contain the solution matrix 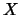 .
.
If
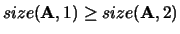 and
and
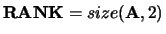 , the residual sum-of-squares for
the solution vector in a column of B is given by the sum of
squares of elements in rows
, the residual sum-of-squares for
the solution vector in a column of B is given by the sum of
squares of elements in rows
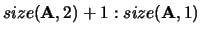 of that column.
of that column.
- RANK
- Optional (output) INTEGER.
The effective rank of  , i.e., the order of the submatrix
, i.e., the order of the submatrix
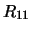 . This is the same as the order of the submatrix
. This is the same as the order of the submatrix 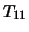 in the complete orthogonal factorization of
in the complete orthogonal factorization of  .
.
- JPVT
- Optional (input/output) INTEGER array,
shape
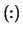 with
with 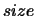 (JPVT)
(JPVT) 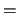
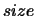 (A,2).
(A,2).
On entry, if
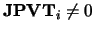 , the
, the  column of
column of
 is an initial column, otherwise it is a free column. Before
the
is an initial column, otherwise it is a free column. Before
the 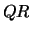 factorization of
factorization of  , all initial columns are
permuted to the leading positions; only the remaining
free columns are moved as a result of column pivoting
during the factorization.
, all initial columns are
permuted to the leading positions; only the remaining
free columns are moved as a result of column pivoting
during the factorization.
On exit, if
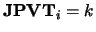 , then the
, then the 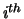 column of
the matrix product
column of
the matrix product 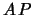 was the
was the  column of
column of  .
.
- RCOND
- Optional (input) REAL.
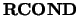 is used to determine the effective rank of
is used to determine the effective rank of  .
This is defined as the order of the largest leading triangular
submatrix
.
This is defined as the order of the largest leading triangular
submatrix 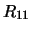 in the
in the 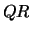 factorization of
factorization of  , with
pivoting, whose estimated condition number
, with
pivoting, whose estimated condition number
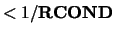 .
.
Default value:
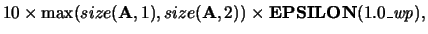 where wp is the working precision.
where wp is the working precision.
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$= 0$:}] successful exit
\item[{$< 0$:}] if ${\bf INFO} = -i$, the $i^{th}$\ argument had an illegal
value
\end{infoarg}](img552.gif)
If 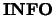 is not present and an error occurs, then the program is
terminated with an error message.
is not present and an error occurs, then the program is
terminated with an error message.
References: [1] and [17,9,20,35].





Next: Example (from Program LA_GELSY_EXAMPLE)
Up: Linear Least Squares Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
![\begin{infoarg}
\item[{$= 0$:}] successful exit
\item[{$< 0$:}] if ${\bf INFO} = -i$, the $i^{th}$\ argument had an illegal
value
\end{infoarg}](img552.gif)
![\begin{infoarg}
\item[{$= 0$:}] successful exit
\item[{$< 0$:}] if ${\bf INFO} = -i$, the $i^{th}$\ argument had an illegal
value
\end{infoarg}](img552.gif)