




Next: Examples
Up: Linear Least Squares Problems
Previous: Purpose
Contents
Index
- A
- (input/output) REAL or COMPLEX
rectangular array, shape
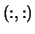 .
.
On entry, the matrix  .
.
On exit, if
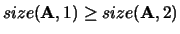 ,
, 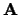 is
overwritten by details of its
is
overwritten by details of its 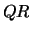 factorization.
If
factorization.
If
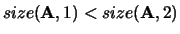 ,
, 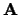 is
overwritten by details of its
is
overwritten by details of its 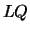 factorization.
factorization.
- B
- (input/output) REAL or COMPLEX array, shape
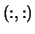 with
with 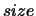 (B,1)
(B,1) 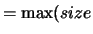 (A,1),
(A,1), 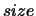 (A,2)) or
shape
(A,2)) or
shape 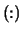 with
with
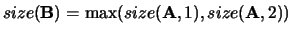 .
.
On entry, the matrix 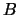 .
.
On exit, the solution matrix X. There are four cases:

- TRANS
- Optional (input) CHARACTER(LEN=1).
Specifies the form of the system of equations:
![\begin{optionarg}
\item[{= 'N':}] $Ax=b$\ (No transpose)
\item[{= 'T':}] $A^Tx=b$\ (Transpose)
\item[{= 'C':}] $A^Hx=b$\ (Conjugate transpose)
\end{optionarg}](img522.gif)
Default value: 'N'.
- INFO
- Optional (output) INTEGER
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO} $= -i$, the $i^{th}$\ argument had an illegal
value.
\end{infoarg}](img523.gif)
If 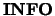 is not present and an error occurs, then the program is
terminated with an error message.
is not present and an error occurs, then the program is
terminated with an error message.
References: [1] and [17,9,20].
Susan Blackford
2001-08-19

![\begin{optionarg}
\item[{= 'N':}] $Ax=b$\ (No transpose)
\item[{= 'T':}] $A^Tx=b$\ (Transpose)
\item[{= 'C':}] $A^Hx=b$\ (Conjugate transpose)
\end{optionarg}](img522.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO} $= -i$, the $i^{th}$\ argument had an illegal
value.
\end{infoarg}](img523.gif)

![\begin{optionarg}
\item[{= 'N':}] $Ax=b$\ (No transpose)
\item[{= 'T':}] $A^Tx=b$\ (Transpose)
\item[{= 'C':}] $A^Hx=b$\ (Conjugate transpose)
\end{optionarg}](img522.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INFO} $= -i$, the $i^{th}$\ argument had an illegal
value.
\end{infoarg}](img523.gif)