




Next: Examples
Up: Symmetric Indefinite Linear Systems
Previous: Purpose
Contents
Index
- AP
- (input/output) REAL or COMPLEX array,
shape
 with
with
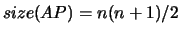 , where
, where 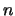 is the order
of
is the order
of  .
.
On entry, the upper or lower triangle of matrix  in packed storage. The
elements are stored columnwise as follows:
in packed storage. The
elements are stored columnwise as follows:
On exit, the block diagonal matrix  and
the multipliers used to obtain
and
the multipliers used to obtain 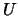 or
or 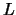 from the factorization of
from the factorization of
 , stored as a packed triangular matrix in the same storage format
as
, stored as a packed triangular matrix in the same storage format
as  .
.
- B
- (input/output) REAL or COMPLEX
array, shape
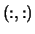 with
with
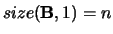 or shape
or shape 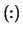 with
with
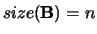 .
.
On entry, the matrix 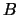 .
.
On exit, the solution matrix 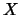 .
.
- UPLO
- Optional (input) CHARACTER(LEN=1)
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
Default value: 'U'.
- IPIV
- Optional (output) INTEGER array, shape
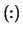 with
with
 .
.
Details of the row and column interchanges and
the block structure of  .
.
If
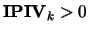 , then rows and columns
, then rows and columns 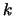 and
and
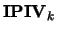 were interchanged, and
were interchanged, and 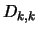 is a
is a
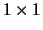 diagonal block.
diagonal block.
If
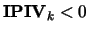 , then there are two cases:
, then there are two cases:

- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit
\item[{$<$\ 0:}] if ${\bf INF...
...l matrix $D$\ is
singular, so the solution could not be computed.
\end{infoarg}](img502.gif)
If INFO is not present and an error occurs, then the program
is terminated with an error message.
References: [1] and [17,9,20,21].





Next: Examples
Up: Symmetric Indefinite Linear Systems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
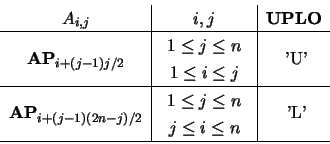
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)

![\begin{infoarg}
\item[{$=$\ 0:}] successful exit
\item[{$<$\ 0:}] if ${\bf INF...
...l matrix $D$\ is
singular, so the solution could not be computed.
\end{infoarg}](img502.gif)