On entry, the upper (if UPLO = 'U') or lower (if UPLO = 'L') triangle of matrix
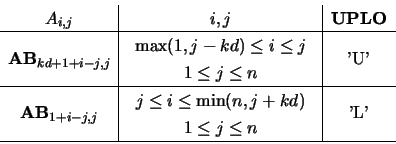
On exit, the factor ![]() or
or ![]() from
the Cholesky factorization
from
the Cholesky factorization
![]() in the same storage format as
in the same storage format as ![]() .
.
On entry, the matrix
On exit, the solution matrix
![\begin{optionarg}
\item[{= 'U':}] Upper triangle of A is stored;
\item[{= 'L':}] Lower triangle of A is stored.
\end{optionarg}](img373.gif)
Default value: 'U'.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...n could not be
completed and the solution could not be computed.
\end{infoarg}](img374.gif)
If INFO is not present and an error occurs, then the program is terminated with an error message.