
To explain s and sep , we need to introduce the spectral projector P [56][72], and the separation of two matrices A and B, sep(A , B) [75][72].
We may assume the matrix A is in Schur form, because reducing it to this form does not change the values of s and sep. Consider a cluster of m > = 1 eigenvalues, counting multiplicities. Further assume the n-by-n matrix A is
where the eigenvalues of the m-by-n matrix
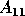 are exactly those in which we are
interested. In practice, if the eigenvalues on the diagonal of A
are in the wrong order, routine xTREXC
can be used to put the desired ones in the upper left corner
as shown.
are exactly those in which we are
interested. In practice, if the eigenvalues on the diagonal of A
are in the wrong order, routine xTREXC
can be used to put the desired ones in the upper left corner
as shown.
We define the spectral projector, or simply projector P belonging
to the eigenvalues of 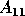 as
as
where R satisfies the system of linear equations
Equation (4.3) is called a Sylvester equation . Given the Schur form (4.1), we solve equation (4.3) for R using the subroutine xTRSYL.
We can now define s for the eigenvalues of 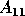 :
:

In practice we do not use this expression since 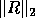 is hard to
compute. Instead we use the more easily computed underestimate
is hard to
compute. Instead we use the more easily computed underestimate

which can underestimate the true value of s by no more than a factor
 .
This underestimation makes our error bounds more conservative.
This approximation of s is called RCONDE in xGEEVX and xGEESX.
.
This underestimation makes our error bounds more conservative.
This approximation of s is called RCONDE in xGEEVX and xGEESX.
The separation 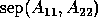 of the matrices
of the matrices 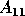 and
and
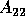 is defined as the smallest singular value of the linear
map in (4.3) which takes X to
is defined as the smallest singular value of the linear
map in (4.3) which takes X to 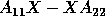 , i.e.,
, i.e.,
This formulation lets us estimate 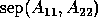 using the condition estimator
xLACON [52][51][48], which estimates the norm of
a linear operator
using the condition estimator
xLACON [52][51][48], which estimates the norm of
a linear operator  given the ability to compute T and
given the ability to compute T and
 quickly for arbitrary x.
In our case, multiplying an
arbitrary vector by T
means solving the Sylvester equation (4.3)
with an arbitrary right hand side using xTRSYL, and multiplying by
quickly for arbitrary x.
In our case, multiplying an
arbitrary vector by T
means solving the Sylvester equation (4.3)
with an arbitrary right hand side using xTRSYL, and multiplying by
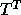 means solving the same equation with
means solving the same equation with 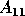 replaced by
replaced by
 and
and 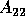 replaced by
replaced by 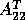 . Solving either equation
costs at most
. Solving either equation
costs at most 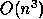 operations, or as few as
operations, or as few as 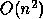 if m << n.
Since the true value of sep is
if m << n.
Since the true value of sep is 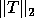 but we use
but we use  ,
our estimate of sep may differ from the true value by as much as
,
our estimate of sep may differ from the true value by as much as
 . This approximation to sep is called
RCONDV by xGEEVX and xGEESX.
. This approximation to sep is called
RCONDV by xGEEVX and xGEESX.
Another formulation which in principle permits an exact evaluation of
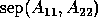 is
is
where  is the Kronecker product of X and Y.
This method is
generally impractical, however, because the matrix whose smallest singular
value we need is m(n - m) dimensional, which can be as large as
is the Kronecker product of X and Y.
This method is
generally impractical, however, because the matrix whose smallest singular
value we need is m(n - m) dimensional, which can be as large as
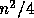 . Thus we would require as much as
. Thus we would require as much as 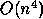 extra workspace and
extra workspace and
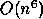 operations, much more than the estimation method of the last
paragraph.
operations, much more than the estimation method of the last
paragraph.
The expression 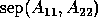 measures the ``separation'' of
the spectra
of
measures the ``separation'' of
the spectra
of 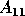 and
and 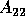 in the following sense. It is zero if and only if
in the following sense. It is zero if and only if
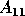 and
and 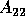 have a common eigenvalue, and small if there is a small
perturbation of either one that makes them have a common eigenvalue. If
have a common eigenvalue, and small if there is a small
perturbation of either one that makes them have a common eigenvalue. If
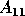 and
and 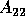 are both Hermitian matrices, then
are both Hermitian matrices, then 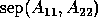 is just the gap, or minimum distance between an eigenvalue of
is just the gap, or minimum distance between an eigenvalue of 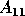 and an
eigenvalue of
and an
eigenvalue of 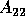 . On the other hand, if
. On the other hand, if 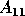 and
and 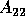 are
non-Hermitian,
are
non-Hermitian, 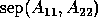 may be much smaller than
this gap.
may be much smaller than
this gap.