Factorizations for Solving Linear Equations





Next: Factorization
Up: Examples of Block
Previous: Examples of Block
The well-known LU and Cholesky factorizations are the simplest block
algorithms to derive. No extra floating-point operations nor extra
working storage are required.
Table 3.3
illustrates the speed of the LAPACK routine for LU factorization of a
real matrix ,
SGETRF in single precision on CRAY machines, and DGETRF in double precision
on all other machines. This corresponds to 64-bit floating-point
arithmetic
on all machines tested. A block size of 1 means that the unblocked algorithm
is used, since it is faster than - or at least as fast as - a
blocked algorithm.
---------------------------------------------------
No. of Block Values of n
processors size 100 1000
---------------------------------------------------
CONVEX C-4640 1 64 274 711
CONVEX C-4640 4 64 379 2588
CRAY C90 1 128 375 863
CRAY C90 16 128 386 7412
DEC 3000-500X Alpha 1 32 53 91
IBM POWER2 model 590 1 32 110 168
IBM RISC Sys/6000-550 1 32 33 56
SGI POWER CHALLENGE 1 64 81 201
SGI POWER CHALLENGE 4 64 79 353
---------------------------------------------------
Table 3.3: Speed in megaflops of SGETRF/DGETRF for square matrices of order n
Table 3.4
gives similar results for Cholesky factorization .
---------------------------------------------------
No. of Block Values of n
processors size 100 1000
---------------------------------------------------
CONVEX C-4640 1 64 120 546
CONVEX C-4640 4 64 150 1521
CRAY C90 1 128 324 859
CRAY C90 16 128 453 9902
DEC 3000-500X Alpha 1 32 37 83
IBM POWER2 model 590 1 32 102 247
IBM RISC Sys/6000-550 1 32 40 72
SGI POWER CHALLENGE 1 64 74 199
SGI POWER CHALLENGE 4 64 69 424
---------------------------------------------------
Table 3.4: Speed in megaflops of SPOTRF/DPOTRF for matrices of order n with UPLO = `U'
LAPACK, like LINPACK, provides a factorization for symmetric
indefinite
matrices, so that A is factorized as 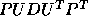 , where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF /DSYTRF .
It has to duplicate a little of the computation in order
to ``look ahead''
to determine the necessary row and column interchanges, but the extra work
can be more than compensated for by the greater speed of updating the matrix
by blocks as is illustrated in Table 3.5 .
, where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF /DSYTRF .
It has to duplicate a little of the computation in order
to ``look ahead''
to determine the necessary row and column interchanges, but the extra work
can be more than compensated for by the greater speed of updating the matrix
by blocks as is illustrated in Table 3.5 .
-------------------
Block Values of n
size 100 1000
-------------------
1 62 86
64 68 165
-------------------
Table 3.5: Speed in megaflops of DSYTRF for matrices of order n with UPLO = `U' on an IBM POWER2 model 590
LAPACK, like LINPACK, provides LU and Cholesky factorizations of
band matrices. The LINPACK algorithms can easily be restructured to use
Level 2 BLAS, though that has little effect on performance for
matrices of very narrow bandwidth. It is also possible to use Level 3 BLAS,
at the price of doing some extra work with zero elements outside the band
[39]. This becomes worthwhile for matrices of large order and
semi-bandwidth greater than 100 or so.





Next: Factorization
Up: Examples of Block
Previous: Examples of Block
Tue Nov 29 14:03:33 EST 1994
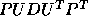 , where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF /DSYTRF .
It has to duplicate a little of the computation in order
to ``look ahead''
to determine the necessary row and column interchanges, but the extra work
can be more than compensated for by the greater speed of updating the matrix
by blocks as is illustrated in Table 3.5 .
, where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF /DSYTRF .
It has to duplicate a little of the computation in order
to ``look ahead''
to determine the necessary row and column interchanges, but the extra work
can be more than compensated for by the greater speed of updating the matrix
by blocks as is illustrated in Table 3.5 .