
The generalized (or quotient) singular value decomposition of an m-by-n matrix A and a p-by-n matrix B is given by the pair of factorizations

The matrices in these factorizations have the following properties:
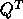 should be
replaced by
should be
replaced by 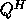 in the pair of factorizations.
in the pair of factorizations.
 , and satisfies r < = n.
, and satisfies r < = n.
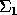 is m-by-r,
is m-by-r,
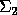 is p-by-r, both are real, nonnegative and diagonal, and
is p-by-r, both are real, nonnegative and diagonal, and
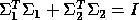 .
Write
.
Write
 and
and
 ,
where
,
where 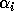 and
and 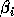 lie in the interval from 0 to 1.
The ratios
lie in the interval from 0 to 1.
The ratios
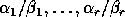 are called the generalized singular values of the pair A,B,
are called the generalized singular values of the pair A,B, 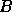 .
If
.
If 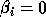 , then the generalized singular value
, then the generalized singular value
 is infinite.
is infinite.
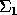 and
and 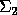 have the following detailed
structures, depending on whether m - r > = 0 or
m - r < 0. In the first case, m - r > = 0, then
have the following detailed
structures, depending on whether m - r > = 0 or
m - r < 0. In the first case, m - r > = 0, then

Here l is the rank of B, m = r - 1, C and S are diagonal
matrices satisfying 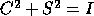 , and S is nonsingular.
We may also identify
, and S is nonsingular.
We may also identify
 ,
,
 for
for  ,
,
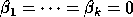 , and
, and
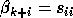 for
for  .
Thus, the first k generalized singular values
.
Thus, the first k generalized singular values
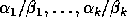 are infinite, and the remaining l generalized singular values
are finite.
are infinite, and the remaining l generalized singular values
are finite.
In the second case, when m - r < 0,
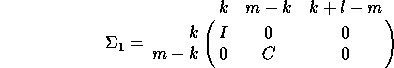
and
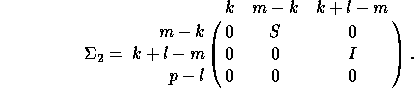
Again, l is the rank of B, k = r - 1, C and S are diagonal
matrices satisfying 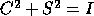 , S is nonsingular,
and we may identify
, S is nonsingular,
and we may identify
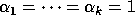 ,
,
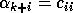 for
for 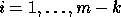 ,
,
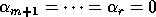 ,
,
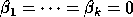 ,
,
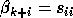 for
for 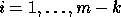 , and
, and
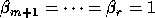 .
Thus, the first
.
Thus, the first 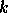 generalized singular values
generalized singular values
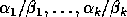 are infinite, and the remaining
are infinite, and the remaining 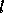 generalized singular values
are finite.
generalized singular values
are finite.
Here are some important special cases of the generalized singular value
decomposition.
First, if B is square and nonsingular, then r = n and the
generalized singular value decomposition of A and B is equivalent
to the singular value decomposition of 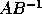 , where the singular
values of
, where the singular
values of 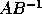 are equal to the generalized singular values of the
pair A,B:
are equal to the generalized singular values of the
pair A,B:

Second, if
the columns of  are orthonormal, then r = n, R = I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of
are orthonormal, then r = n, R = I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of  [45]:
[45]:
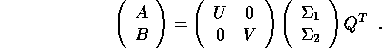
Third, the generalized eigenvalues and eigenvectors of 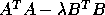 can be expressed in terms of the generalized singular value decomposition:
Let
can be expressed in terms of the generalized singular value decomposition:
Let
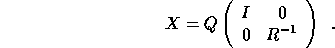
Then
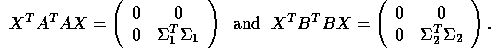
Therefore, the columns of X are the eigenvectors of
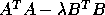 , and the ``nontrivial'' eigenvalues are the
squares of the generalized singular values (see also section 2.2.5.1).
``Trivial'' eigenvalues
are those corresponding to the leading n - r columns of X,
which span the common null space of
, and the ``nontrivial'' eigenvalues are the
squares of the generalized singular values (see also section 2.2.5.1).
``Trivial'' eigenvalues
are those corresponding to the leading n - r columns of X,
which span the common null space of 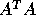 and
and  .
The ``trivial eigenvalues'' are not well defined
.
The ``trivial eigenvalues'' are not well defined![]() .
.
A single driver routine xGGSVD computes the generalized singular value decomposition of A and B (see Table 2.6). The method is based on the method described in [12][10][62].
----------------------------------------------------------------
Type of Function and Single precision Double precision
problem storage scheme real complex real complex
----------------------------------------------------------------
GSEP simple driver SSYGV CHEGV DSYGV ZHEGV
simple driver SSPGV CHPGV DSPGV ZHPGV
(packed storage)
simple driver SSBGV CHBGV DSBGV ZHBGV
(band matrices)
----------------------------------------------------------------
GNEP simple driver for SGEGS CGEGS DGEGS ZGEGS
Schur factorization
simple driver for SGEGV CGEGV DGEGV ZGEGV
eigenvalues/vectors
----------------------------------------------------------------
GSVD singular values/ SGGSVD CGGSVD DGGSVD ZGGSVD
vectors
-----------------------------------------------------------------
Table 2.6: Driver routines for generalized eigenvalue and singular value problems