Singular Value Decomposition (SVD)


next up previous contents index
Next: Generalized Eigenvalue and Up: Standard Eigenvalue and Previous: Nonsymmetric Eigenproblems (NEP)

Singular Value Decomposition (SVD)

The singular value decomposition of an m-by-n matrix A is given by   

where U and V are orthogonal (unitary) and is an m-by-n diagonal matrix with real diagonal elements, 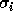, such that

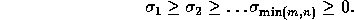
The 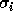are the singular values of A and the first min(m , n) columns of U and V are the left and right singular vectors of A.   

The singular values and singular vectors satisfy:

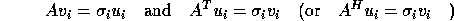
where and 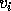are the i-th columns of U and V respectively.

A single driver  routine xGESVD     computes all or part of the singular value decomposition of a general nonsymmetric matrix (see Table 2.5).   A future version of LAPACK will include a driver based on divide and conquer, as in section 2.2.4.1. 

--------------------------------------------------------------------------
Type of                                 Single precision  Double precision
problem  Function and storage scheme    real     complex  real     complex
--------------------------------------------------------------------------
SEP      simple driver                  SSYEV    CHEEV    DSYEV    ZHEEV
         expert driver                  SSYEVX   CHEEVX   DSYEVX   ZHEEVX
--------------------------------------------------------------------------
         simple driver (packed storage) SSPEV    CHPEV    DSPEV    ZHPEV
         expert driver (packed storage) SSPEVX   CHPEVX   DSPEVX   ZHPEVX
--------------------------------------------------------------------------
         simple driver (band matrix)    SSBEV    CHBEV    DSBEV    ZHBEV
         expert driver (band matrix)    SSBEVX   CHBEVX   DSBEVX   ZHBEVX
--------------------------------------------------------------------------
         simple driver (tridiagonal     SSTEV             DSTEV   
          matrix)

         expert driver (tridiagonal     SSTEVX            DSTEVX  
          matrix)
--------------------------------------------------------------------------
NEP      simple driver for              SGEES    CGEES    DGEES    ZGEES
          Schur factorization

         expert driver for              SGEESX   CGEESX   DGEESX   ZGEESX
          Schur factorization

         simple driver for              SGEEV    CGEEV    DGEEV    ZGEEV
          eigenvalues/vectors

         expert driver for              SGEEVX   CGEEVX   DGEEVX   ZGEEVX
          eigenvalues/vectors
--------------------------------------------------------------------------
SVD      singular values/vectors        SGESVD   CGESVD   DGESVD   ZGESVD
--------------------------------------------------------------------------

Table 2.5: Driver routines for standard eigenvalue and singular value problems



Tue Nov 29 14:03:33 EST 1994